¿Escala categórica o continua para gráfico de área?

Question

Me gustaría trazar el adjunto como un gráfico de áreas: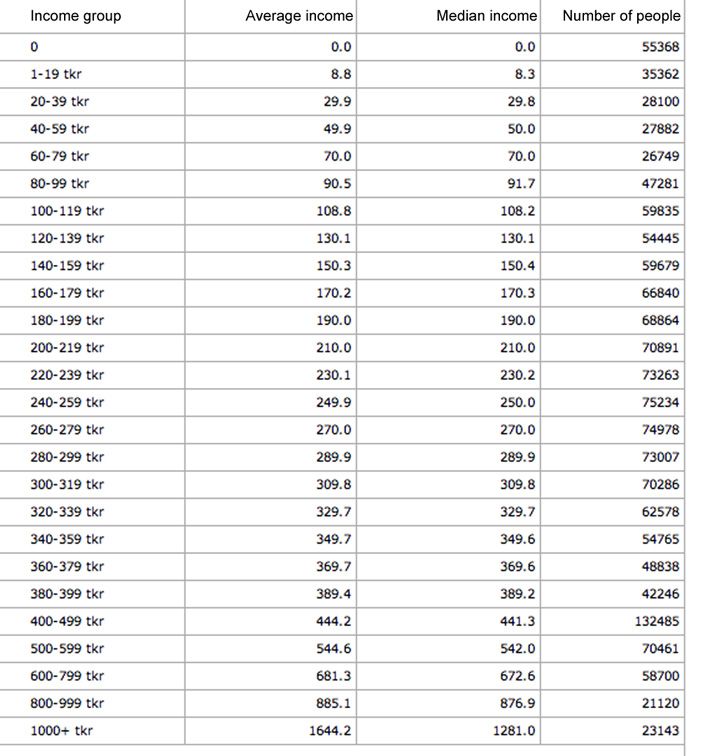

Como puedes ver, los ingresos personales se dividen en 26 intervalos de diferentes anchos. También tengo la media y la mediana de ingresos en los intervalos.

Para transmitir gráficamente de manera veraz estos datos, me pregunto cuáles son realmente mis opciones.
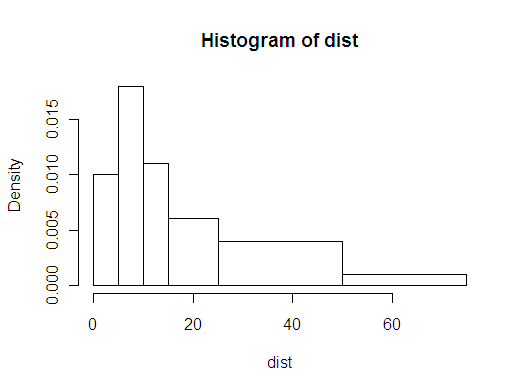
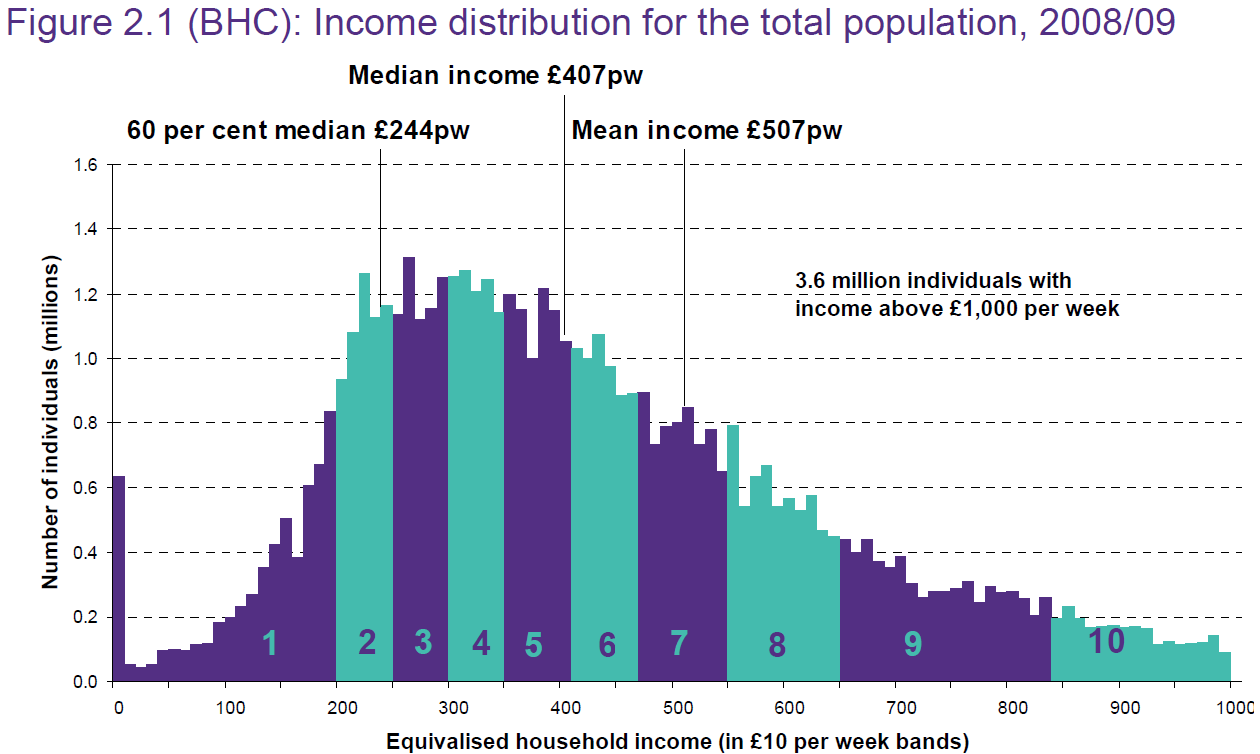
Trazando los datos categóricos ordinales disponibles se obtendría un gran montículo en el gráfico de áreas para el intervalo de 400-499. Pero esto se debe solamente a que ese intervalo es más ancho y el usuario podría ser engañado por la forma. Otro problema con los datos categóricos es que el promedio del intervalo "1000+" está muy lejos de 1000 (= 1644). Un gráfico de áreas que no tenga en cuenta esto haría un mal trabajo mostrando la distribución real.

¿Cómo te las arreglarías y hay alguna manera en la que pueda utilizar la media/mediana para "convertir la escala categórica en una escala continua"?

Answer 1

Esto no es exactamente lo que pediste, pero aún puede ser útil.

Puedes confiar en el comando plot.histogram en R. El uso habitual es ejecutar un comando hist, que prepara un objeto de clase histogram y lo pasa a plot.histogram. Puedes preparar un objeto histogram personalizado y trazarlo con plot.histogram.

El siguiente código imprime un objeto histogram:

data(cars); dput(hist(cars$dist, plot=FALSE))

Puedes hacer un objeto similar y trazarlo:

k = structure(list(breaks = c(0, 5, 10, 15, 25, 50, 75), counts = NULL,
  intensities = NULL, density = c(0.01, 0.018, 0.011, 0.006, 0.004, 
  0.001), mids = NULL, xname = "dist", equidist = FALSE), .Names = c("breaks", 
  "counts", "intensities", "density", "mids", "xname", "equidist"
  ), class = "histogram")
plot(k)

Answer 2

Un histograma con una escala continua como la descrita por GaBorgulya es claramente la forma de proceder. Cuando los bloques son más anchos, es necesario ajustar la densidad apropiadamente: el bloque 380-399 con 42246 personas debería tener aproximadamente 1.6 veces la densidad del bloque 400-499 con 132485 personas.

Exceptuando los extremos de 0 y 1000+, puedes simplemente utilizar los bloques que tienes, con las densidades (número de personas dividido por el ancho del bloque) como altura. Puedes acercarte aún más a la distribución dividiendo cada bloque en las medianas: así, por ejemplo, tienes 58700 en el intervalo "600 a 799 tkr" (es decir, casi 800), para una densidad de 293.5. O podrías dividir esto en la mediana de 681.3 en dos bloques representando 29350 cada uno, para tener un intervalo de 600 a 672.6 con una densidad de 404.3 y un intervalo de 672.6 a 800 con una densidad de 230.4. Podrías ir más lejos y también tener en cuenta las medias en cada intervalo, pero no creo que sea una prioridad.

El extremo de 1000+ (23143 personas, mediana 1281.0, media 1644.2) es un poco más complicado pero puedes usar la mediana para darte un intervalo de 1000 a 1281 con una densidad de 41.2. Ahora vale la pena usar la media. Por ejemplo podrías tener el intervalo superior de 1281 a 3014.8 con una densidad de 6.7. Esto no es realista ya que el ingreso máximo probablemente sea mayor que 3014.8 y es probable que la curva esté disminuyendo en lugar de plana, pero ilustra el problema.

Ilustrar el extremo en 0 es aún más complicado. Dependiendo de qué tan ancho hagas el bloque, puedes tener un pico tan alto como desees. Aquí hay un ejemplo de _Hogares por Debajo del Ingreso Promedio_ donde utilizaron bloques de £10. Tiene otras características de diseño, algunas de las cuales te pueden resultar interesantes, como un corte en el extremo superior y palabras describiendo cuántos fueron cortados.