¿Implica la expansión del espacio que la luz *nunca* alcanzará objetos actualmente lo suficientemente distantes?

Question

Supongamos que dos objetos están aproximadamente a una distancia de aproximadamente el doble de la Distancia de Hubble entre ellos. Uno de ellos emite luz hacia el otro.

Cuando la luz emitida desde uno alcanza la Distancia de Hubble desde su origen (dentro de un tiempo menor al Tiempo de Hubble, pero más de la mitad de éste) el otro estará a más de otra Distancia de Hubble más lejos del primero que al principio - la distancia desde el punto que alcanzó la luz será mayor que al inicio del recorrido.

¿Es eso correcto o estoy perpetuando otro malentendido relacionado con la Expansión del Espacio?

Answer 1

Su texto es un poco confuso, pero la respuesta a la pregunta en su título es sí. Existe una distancia llamada el horizonte de sucesos cósmico. Si las galaxias más allá de esta distancia emiten luz hoy, entonces esta luz nunca nos alcanzará. Así es como se puede calcular el horizonte de sucesos:

La expansión del universo se puede describir por el factor de escala $a(t)$, que aumenta de 0 en el Big Bang a 1 en el día de hoy, y a infinito a medida que el universo envejece. Los varios componentes del universo (radiación, materia y energía oscura) determinan la tasa de expansión de una manera específica, que se expresa por el parámetro de Hubble $$ H(a) = \frac{\dot{a}}{a} = H_0\sqrt{\Omega_{R,0}\,a^{-4} + \Omega_{M,0}\,a^{-3} + \Omega_{K,0}\,a^{-2} + \Omega_{\Lambda,0}}, $$ con $$ \begin{gather} H_0 = 67.3\;\text{km}\,\text{s}^{-1}\text{Mpc}^{-1},\quad \Omega_{R,0}\approx 0, \\ \Omega_{M,0} = 0.315,\quad \Omega_{\Lambda,0} = 0.685, \quad \Omega_{K,0} = 0, \end{gather} $$ según los resultados más recientes del Planck. Ahora, para calcular distancias, necesitamos crear un sistema de coordenadas. Los cosmólogos utilizan los llamados coordenadas co-móviles, que es una cuadrícula de coordenadas que se expande junto con el universo. Esto significa que una galaxia lejana tiene una distancia co-móvil fija $D_c$, mientras que su distancia propia aumenta con el tiempo de la siguiente manera $$ D(t) = a(t)D_c. $$ En la edad cósmica actual $t_0$, tenemos $a(t_0)=1$, y ambas distancias coinciden. Si $\text{d}\ell$ es una distancia co-móvil infinitesimal, entonces un fotón viajará en un intervalo de tiempo $\text{d}t$ una distancia propia $$ c\,\text{d}t = a(t)\text{d}\ell, $$ así que $$ \text{d}\ell = \frac{c\,\text{d}t}{a(t)} = \frac{c\,\text{d}a}{a\,\dot{a}} = \frac{c\,\text{d}a}{a^2\,H(a)} = \frac{c\,\text{d}a}{\sqrt{\Omega_{R,0} + \Omega_{M,0}\,a + \Omega_{K,0}\,a^2 + \Omega_{\Lambda,0}\,a^4}}. $$ Integrando esto, obtenemos la distancia co-móvil recorrida por un fotón, emitido desde una fuente en el tiempo $t_\text{em}$ y observado por nosotros en el tiempo $t_\text{ob}$: $$ D_c = \frac{c}{H_0}\int_{a(t_\text{em})}^{a(t_\text{ob})}\frac{\text{d}a}{\sqrt{\Omega_{R,0} + \Omega_{M,0}\,a + \Omega_{K,0}\,a^2 + \Omega_{\Lambda,0}\,a^4}}. $$ Ahora, el horizonte de sucesos cósmico en el tiempo $t$ se define de la siguiente manera: si una fuente en el horizonte de sucesos cósmico emite un fotón en el tiempo $t$, este fotón nos alcanzará en el tiempo $t=\infty$, por lo que la distancia co-móvil del horizonte de sucesos es $$ D_{c,\text{eh}}(t) = \frac{c}{H_0}\int_{a(t)}^{\infty}\frac{\text{d}a}{\sqrt{\Omega_{R,0} + \Omega_{M,0}\,a + \Omega_{K,0}\,a^2 + \Omega_{\Lambda,0}\,a^4}}, $$ y la distancia propia correspondiente es $D_{\text{eh}}(t) = a(t)D_{c,\text{eh}}(t)$. Esto significa que todos los fotones emitidos por galaxias dentro del horizonte en el tiempo $t$ eventualmente nos alcanzarán, pero los fotones emitidos fuera del horizonte nunca nos alcanzarán.

Estos gráficos deberían aclarar las cosas (haz clic en 'ver imagen' para una versión más grande):

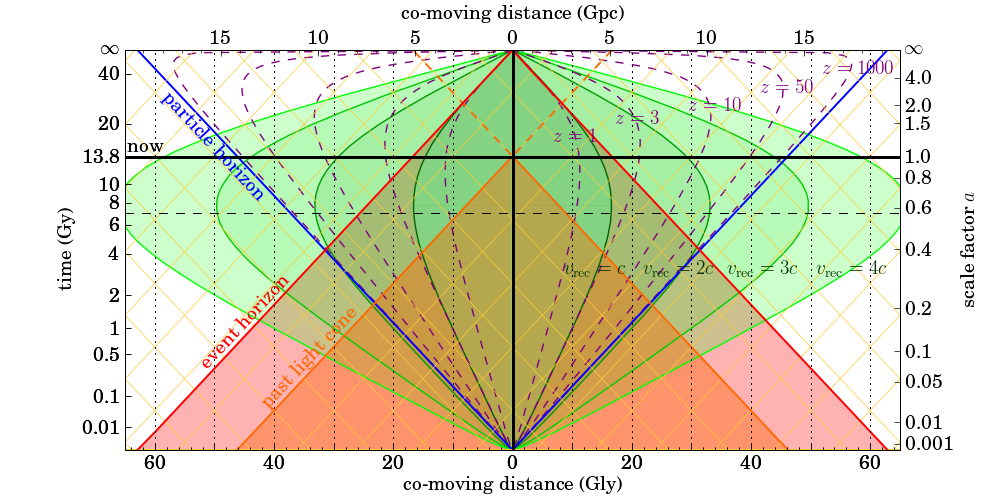
En el eje horizontal, tenemos la distancia co-móvil de las fuentes de luz, en Gigalightyears (abajo) y los Gigaparsecs correspondientes (arriba). El eje vertical muestra la edad del universo (izquierda) y el factor de escala correspondiente $a$ (derecha). La línea negra horizontal gruesa marca la edad actual del universo (13.8 mil millones de años). Las fuentes de luz co-móviles tienen una distancia co-móvil constante, de modo que sus líneas del mundo son líneas verticales (las líneas punteadas negras corresponden a fuentes en 10, 20, 30, etc Gly). Nuestra propia línea del mundo es la línea vertical negra gruesa, y actualmente nos encontramos en la intersección de la línea negra horizontal y vertical.

Las curvas verdes son líneas de velocidad de recesión constante: el área verde oscuro es la esfera de Hubble, con radio co-móvil $$ D_{c,H}(t) = \frac{c}{a(t)\,H(a(t))}, $$ y las áreas verdes más brillantes son el doble, triple y cuádruple de la esfera de Hubble. Las líneas amarillas son geodésicas nulas, es decir, los caminos de los fotones. La escala del eje de tiempo es tal que estos caminos de fotones son líneas rectas en ángulos de 45°. La línea azul marca el borde del universo observable, es decir, la región del universo que podemos ver (que actualmente tiene un radio de 46.2 mil millones de años luz). Y finalmente, la línea recta roja es el horizonte de sucesos cósmico.

Puedes ver que los fotones dentro del horizonte de sucesos pueden cruzar la línea negra vertical, es decir, pueden alcanzarnos; los fotones fuera no pueden. También nota que la esfera de Hubble está dentro del horizonte de sucesos (y se acercará asintóticamente a él a medida que $t$ tiende a infinito). La distancia de Hubble actual es de 14.5 Gly, mientras que la distancia actual al horizonte de sucesos es de 16.7 Gly. Los fotones emitidos hoy por fuentes que se encuentran entre estas dos distancias todavía nos alcanzarán en el futuro. Por lo tanto, el radio de Hubble en sí mismo no es un horizonte.

El horizonte de sucesos en $t=0$ es de $D_{c,\text{eh}}(0) = 62.9$ mil millones de años luz. Esto significa que las galaxias más allá de esta distancia nunca han podido enviarnos fotones, y nunca podrán hacerlo. Por lo tanto, estas galaxias siempre estarán fuera de nuestro universo observable.

Si usamos distancias propias en lugar de distancias co-móviles, entonces el gráfico se ve así:

Nuevamente, el horizonte de sucesos es la curva roja de tipo parabólico, las galaxias se mueven en las líneas punteadas negras, y los fotones siguen los caminos amarillos. Aquí, puedes ver que un fotón emitido fuera del radio de Hubble pero dentro del horizonte de sucesos primero se alejará de nosotros (porque la velocidad de recesión de la fuente es mayor que $c$), pero eventualmente podrá superar la expansión y comenzar a moverse hacia nosotros. La trayectoria resultante de estos fotones es una forma parecida a una lágrima. Pero los fotones emitidos fuera del horizonte de sucesos no pueden superar la expansión, y siempre se alejarán de nosotros.

Si deseas obtener aún más detalles, consulta este post.

Answer 2

No, no implica eso. Hay modelos cosmológicos que son espacialmente infinitos (y por lo tanto tienen velocidades de recesión arbitrariamente más altas que $c$) en los cuales la luz emitida en cualquier momento desde cualquier punto en el universo eventualmente llegará a cualquier otro punto en el universo.

De hecho, todos los modelos cosmológicos abiertos sin energía oscura tienen esa propiedad.

Por ejemplo, en un modelo dominado por materia de densidad crítica, el factor de escala $a$ crece como $a(t) \sim t^{2/3}$, por lo que la velocidad de la luz en coordenadas de FLRW es $c/a(t) \sim t^{-2/3}$, y $\int_{t_0}^\infty t^{-2/3}\,\mathrm dt = \infty$ para cualquier $t_0$, por lo que con suficiente tiempo, la luz emitida desde cualquier punto en el espacio tiempo cruzará las líneas del mundo de objetos arbitrariamente distantes moviéndose con el flujo de Hubble.

(Estoy bastante seguro de que eventualmente llegará a objetos arbitrariamente distantes que no se mueven con el flujo de Hubble también, siempre y cuando se estén moviendo a menos de la velocidad de la luz y no se alejen para siempre, pero soy demasiado perezoso para intentar demostrarlo ahora mismo.)

En el modelo ΛCDM que parece describir nuestro mundo, hay un límite en cuánto puede viajar la luz, porque el factor de escala eventualmente crece exponencialmente, y $\int_{t_0}^\infty e^{-kt}\,\mathrm dt$ es finito. Sin embargo, la frontera entre lo que podremos y no podremos ver no es la distancia de Hubble, como explica detalladamente la respuesta de Pulsar.

En el futuro lejano, cuando el espacio sea esencialmente de Sitter, la distancia de Hubble coincide con el horizonte de eventos. Pero ese es el único caso del que tengo conocimiento en el cual la distancia de Hubble puede ser asignada alguna interpretación física directa. E incluso ese es filosóficamente dudoso ya que el espacio de Sitter es un vacío simétrico en el tiempo. No creo que una civilización que surgiera en un futuro lejano similar a de Sitter tendría razón alguna para concluir que el universo está expandiéndose, y mucho menos para inventar la ley de Hubble y conceptos asociados.