Esto no responde a su pregunta, pero puede que le da cierta intuición de por qué esto es cierto. Dado el hecho de que exista una solución a la ecuación de $x^2-Py^2=-1$ al $P\equiv 1(\mod 4)$, uno ve que la matriz de
$$
\begin{pmatrix}x & Py \\\ y & x\end{pmatrix}
$$
corrige $\pm\sqrt{P}$ (bajo la acción de $PGL_2(\mathbb{Z})$$\mathbb{RP}^1=\partial_{\infty} \mathbb{H}^2$). La clase conjugacy de una primitiva de la matriz en $GL_2(\mathbb{Z})$ (que no es reducible o finito de orden) se determina por la cerrada geodésica en el sistema modular de orbifold que representa. Este a su vez está determinado por una secuencia de triángulos que la geodésica cruces en la Farey gráfico:
![alt text]() Estos triángulos vienen en racimos compartir un vértice común, donde el número en cada racimo corresponde a los coeficientes de la continuación de la fracción de expansión.
La matriz es conjugado a $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ si el determinante es 1, y para
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.
Estos triángulos vienen en racimos compartir un vértice común, donde el número en cada racimo corresponde a los coeficientes de la continuación de la fracción de expansión.
La matriz es conjugado a $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ si el determinante es 1, y para
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.
![alt text]()
[Nota: las etiquetas en esta figura no se corresponden exactamente con las matrices - debería ser $a_i$'s en lugar de $\alpha_i$'s, y $\alpha_{\pm}$ debe $\pm\sqrt{P}$]
El número de tales factores se corresponden exactamente con el período de la continuación de la fracción de expansión de puntos fijos de la matriz, ya que el cerrado geodésica es asintótica en $\mathbb{H}^2$ a de la línea geodésica conectar $\infty$$\sqrt{P}$, cuya secuencia de Farey da lugar a la continuación de la fracción de expansión de $\sqrt{P}$.
Este número es par si y sólo si la matriz es la orientación de la conservación, que es si y sólo si el determinante es 1. Por lo que el factor determinante es $1$ si y sólo si la continuación de la fracción tiene aún período, y el factor determinante es $-1$ si y sólo si la continuación de la fracción tiene impar período, correspondiente a $P\equiv 1(\mod 4)$.

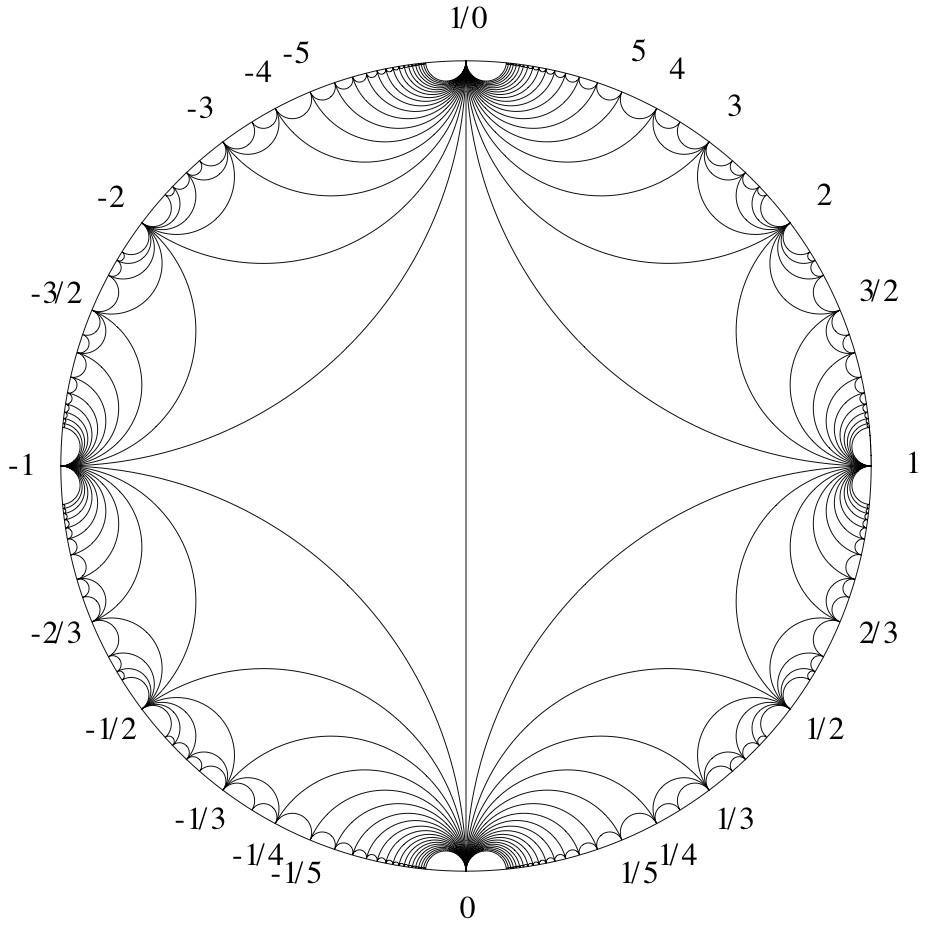 Estos triángulos vienen en racimos compartir un vértice común, donde el número en cada racimo corresponde a los coeficientes de la continuación de la fracción de expansión.
La matriz es conjugado a $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ si el determinante es 1, y para
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.
Estos triángulos vienen en racimos compartir un vértice común, donde el número en cada racimo corresponde a los coeficientes de la continuación de la fracción de expansión.
La matriz es conjugado a $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ si el determinante es 1, y para
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.


