Considere la función $f(x) = ax(1-x)$. Tengo que mostrar que si $ 1 < a < 3$ que el punto fijo, $p_2 = \dfrac{a-1}{a}$ es atractivo, y si $ 3 < a < 4$ es repulsivo.
No tengo idea de cómo hacerlo. He encontrado que la parte superior de la función en $ ( \dfrac{1}{2}, \dfrac{a}{4} )$ y he encontrado que $f'(0) = a$$f'(\dfrac{a-1}{a}) = 2-a$, pero no sé qué hacer con esto.
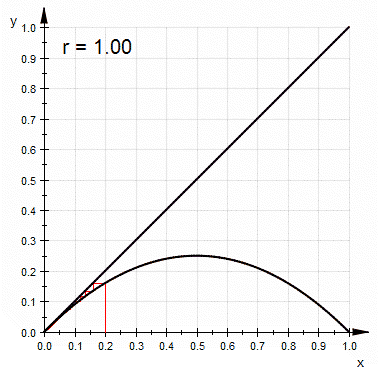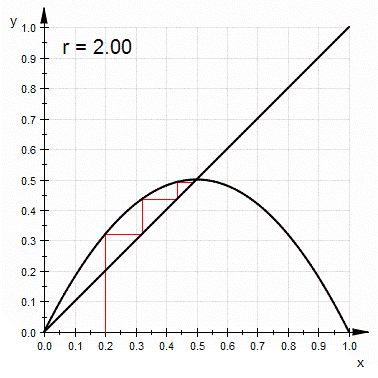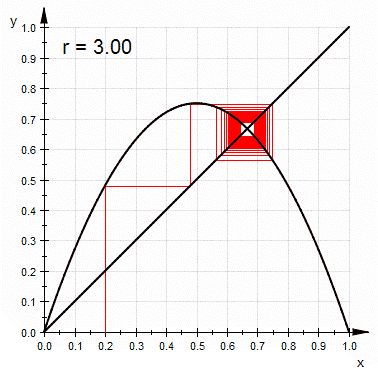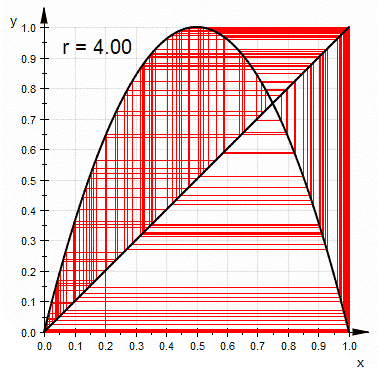
Su función es la de un 'logística mapa' y el truco es comparar el $|f'(p_2)|$$1$. De Wikipedia que han hecho :
"Si la función $f$ es continuamente diferenciable en un abierto de vecindad de un punto fijo $x_0$, e $|f'(x_0)|<1$, la atracción está garantizada".
En este enlace a la Wikipedia, la imagen puede dar una explicación intuitiva (advertencia de la escala vertical es un poco demasiado larga). Las iteraciones de inicio en $x=-1$ y convergen claramente a la derecha : ahora supongamos que la línea vertical a la derecha bajaba un poco más (suponiendo que la pendiente es más pronunciada con $\ f'(x_0)<-1\ $), a continuación, nos gustaría ir más lejos que estábamos en la parte superior y se van al límite en lugar de aproximarse a como lo hacemos aquí (la espiral sería divergente).
Se encuentra a $\ f'\left(\dfrac{a-1}{a}\right) = 2-a$
Pero para $\ 1<a<3\ $ tenemos $\ 2-3<2-a<2-1\ $ y obtener que $\ \left|f'\left(\dfrac{a-1}{a}\right)\right|<1$
El repulsivo parte será manejada de la misma manera.
Por cierto, la Wikipedia tiene una bonita animación cuando el valor de $a$ cambios.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
