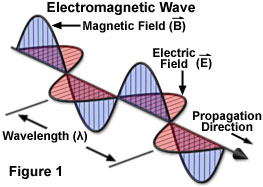
Las imágenes que estamos viendo son correctos, los campos eléctrico y magnético llegar a sus amplitudes y ceros en las mismas ubicaciones. Rafael de la respuesta y algunos comentarios sobre ella son completamente correctos; la conservación de la energía hace que no requieren que la densidad de energía de ser la misma en cada punto de la onda electromagnética. Los puntos donde no hay ningún campo no llevan ningún tipo de energía. Pero nunca hay un momento cuando los campos que vaya a cero en todas partes. De hecho, la onda de siempre mantiene la misma forma de los picos y valles (un sitio ideal para una sola frecuencia de la onda en un perfecto clásica de vacío), por lo que la misma cantidad de energía que siempre está ahí. Sólo se mueve.
Para agregar a Rafael excelente respuesta, he aquí un ejemplo claro.
Considere la posibilidad de una sinusoidal onda electromagnética que se propaga en el $z$ dirección. Tendrá un campo eléctrico dado por
$$\mathbf{E}(\mathbf{r},t) = E_0\hat{\mathbf{x}}\sin(kz - \omega t)$$
Tomar el rizo de este y se obtiene
$$\nabla\times\mathbf{E}(\mathbf{r},t) = \left(\hat{\mathbf{z}}\frac{\partial}{\partial y} - \hat{\mathbf{y}}\frac{\partial}{\partial z}\right)E_0\sin(kz - \omega t) = -E_0 k\hat{\mathbf{y}}\cos(kz - \omega t)$$
Utilizando una de las ecuaciones de Maxwell, $\nabla\times\mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$, se obtiene
$$-\frac{\partial\mathbf{B}(\mathbf{r},t)}{\partial t} = -E_0 k\hat{\mathbf{y}}\cos(kz - \omega t)$$
La integración de esta con respecto al tiempo para encontrar el campo magnético,
$$\mathbf{B}(\mathbf{r},t) = -\frac{E_0 k}{\omega}\hat{\mathbf{y}}\sin(kz - \omega t)$$
Comparando esto con la expresión de $\mathbf{E}(\mathbf{r},t)$, se encuentra que las $\mathbf{B}$ es directamente proporcional a $\mathbf{E}$. Cuando y donde uno es cero, el otro también será cero; cuando y donde uno alcanza su máximo/mínimo, lo hace el otro.
Para una onda electromagnética en el espacio libre, la conservación de la energía se expresa por el teorema de Poynting,
$$\frac{\partial u}{\partial t} = -\nabla\cdot\mathbf{S}$$
El lado izquierdo de esta le da la tasa de cambio de la densidad de energía en el tiempo, donde
$$u = \frac{1}{2}\left(\epsilon_0 E^2 + \frac{1}{\mu_0}B^2\right)$$
y a la derecha dice que la energía electromagnética de la densidad de flujo, en términos del vector de Poynting,
$$\mathbf{S} = \frac{1}{\mu_0}\mathbf{E}\times\mathbf{B}$$
El teorema de Poynting dice que la tasa a la cual la densidad de energía en un punto que cambia es el opuesto de la tasa a la cual la densidad de energía de flujos de distancia de ese punto.
Si el enchufe en las expresiones explícitas para la onda en mi ejemplo, después de un poco de álgebra encontrar
$$\frac{\partial u}{\partial t} = -\omega E_0^2\left(\epsilon_0 + \frac{k^2}{\mu_0\omega^2}\right)\sin(kz - \omega t)\cos(kz - \omega t) = -\epsilon_0\omega E_0^2 \sin\bigl(2(kz - \omega t)\bigr)$$
(el uso de $c = \omega/k$) y
$$\nabla\cdot\mathbf{S} = \frac{2}{\mu_0}\frac{k^2}{\omega}E^2 \sin(kz - \omega t)\cos(kz - \omega t) = \epsilon_0 \omega E_0^2 \sin\bigl(2(kz - \omega t)\bigr)$$
lo que confirma que la igualdad en el teorema de Poynting se mantiene, y por lo tanto que EM la energía se conserva.
Observe que las expresiones a ambos lados de la ecuación incluyen el factor de $\sin\bigl(2(kz - \omega t)\bigr)$ - que no son constantes. Este matemáticamente se muestra la estructura de la energía en una onda EM. No es sólo un uniforme de "la columna de la energía;" la cantidad de energía contenida en la onda varía sinusoidalmente de punto a punto ($S$ le dice que), y a medida que la onda pasa de un punto particular en el espacio, la cantidad de energía que tiene en ese punto varía sinusoidalmente en el tiempo ($u$ le dice que). Pero los cambios en la energía con respecto al espacio y el tiempo no acaba de salir de la nada. Son precisamente sincronizados en la manera especificada por el teorema de Poynting, por lo que los cambios en la energía en un punto se explica por el flujo y de los vecinos de puntos.