¿Cuál es la definición precisa de una forma rígida?

Question

La sección de Wikipedia sobre formas rígidas no parece definir realmente lo que es una forma rígida. En cambio, define 'misma forma' y 'transformaciones rígidas' sin dar ninguna definición de lo que es necesario y suficiente para que una forma se considere rígida.

Por ejemplo, he visto la siguiente imagen:

Entiendo intuitivamente por qué el triángulo es rígido y el cuadrilátero no rígido. También entiendo que insertar una sola conexión diagonal en el cuadrilátero haría que la forma sea rígida? Sin embargo, dada la siguiente imagen (etiquetando las formas $S_1$, $S_2$ y $S_3$ en secuencia de izquierda a derecha):

Si $S_1$ tuviera una sola conexión diagonal AB, sería posible voltear ADB sobre el eje q para obtener una forma similar a $S_2$ con la adición de la conexión AB (mi explicación puede que no sea la mejor). Esta forma claramente no es la misma que $S_1$, entonces ¿cómo podemos decir que $S_1$ con una sola conexión diagonal CD es rígida? Siento que no tengo claro cuál es la definición de rigidez realmente.

Answer 1

Aunque la respuesta aceptada de rschwieb es excelente, creo que hay una conexión entre la noción matemática de "movimiento rígido" y la noción física de "rigidez estructural" que aún no se ha mencionado.

Definamos un diagrama como cualquier colección finita de segmentos de línea con puntos finales etiquetados en el plano. Supongamos que tenemos dos tipos de datos sobre un diagrama dado: sus relaciones de incidencia (es decir, saber qué puntos son los puntos finales de cuáles segmentos de línea) y sus mediciones lineales (es decir, saber cuán largos son los segmentos). Nos hacemos la siguiente pregunta:

¿Está completamente especificado un diagrama por sus relaciones de incidencia y sus medidas lineales?

Otra forma (un poco menos formal) de decir esto es: si conoces cuán largos son todos los segmentos en un diagrama, ¿puedes dibujar el diagrama?

Primero, notemos que lo mejor que podríamos hacer es decir que un diagrama está completamente especificado hasta un movimiento rígido. Es decir, incluso si pudiéramos reconstruir un diagrama a partir de sus relaciones de incidencia y medidas lineales, no sabríamos dónde ubicarlo en el plano o cómo orientarlo, porque un movimiento rígido del plano preserva todas las propiedades de incidencia y métricas mientras posiblemente cambia la posición y la orientación.

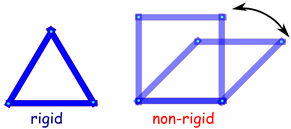
Pero una observación más significativa es que conocer las relaciones de incidencia y las medidas lineales de un diagrama no, en general, especifica completamente un diagrama. Para ver esto, solo hay que mirar el ejemplo en la pregunta original de una forma "no rígida": un cuadrado que se deforma en un rombo. El diagrama original (el cuadrado) y el diagrama deformado (el rombo) tienen exactamente las mismas relaciones de incidencia y medidas lineales, pero los ángulos en ellos son diferentes.

Podemos tomar esto como una caracterización matemática de la noción física de "rigidez estructural": si un diagrama está completamente determinado (hasta un movimiento rígido) por sus relaciones de incidencia y sus medidas lineales, podemos llamarlo un diagrama rígido.

Ahora considera un triángulo. Supongamos que conocemos las longitudes de los tres lados de un triángulo dado $\Delta ABC$. ¿Es posible reconstruir todo lo demás sobre el triángulo?

La respuesta es sí. Esto se conoce como la propiedad Lado-Lado-Lado. En geometría de secundaria, generalmente se formula como un criterio para demostrar que dos triángulos son congruentes:

Si $\Delta ABC$ y $\Delta PQR$ son dos triángulos con $AB=PQ, BC=QR$ y $AC=PR$, entonces $\Delta ABC \cong \Delta PQR$.

La propiedad Lado-Lado-Lado te dice que si los lados de un triángulo son no deformables, entonces sus ángulos están completamente "bloqueados", es decir, el triángulo entero es rígido.

Nota que esto no es cierto para ningún polígono que no sea un triángulo: no hay un criterio de congruencia "Lado-Lado-Lado-Lado" para cuadriláteros.

Ahora consideremos los ejemplos en la pregunta original. El diagrama $S_1$, sin las diagonales punteadas, es un cuadrilátero $ADBC$. Este tipo de cuadrilátero no es rígido, porque se puede dibujar otro cuadrilátero $A'D'B'C'$ con todas las longitudes correspondientes exactamente iguales pero con ángulos interiores diferentes.

Sin embargo, si agregas incluso un segmento de los punteados (por ejemplo, $\overline{DC}$) en el diagrama, entonces el diagrama sería rígido, porque los triángulos $\Delta ADC$ y $\Delta BDC$ son rígidos.

Exactamente las mismas observaciones se aplican a $S_2$.

Para $S_3$, la pregunta de si el diagrama es rígido o no depende de si la línea que parece unir $A$ con $C$ y la línea que parece unir $B$ con $D$ es realmente un segmento, y si así fuera si el punto que parece estar en la intersección de esos segmentos (llamémosle $P$) es explícitamente parte del diagrama o no, y si $\overline{AP}, \overline{PC},$ etc. son todos parte del diagrama. (Observa que todo esto está contenido en la especificación de "relaciones de incidencia" de un diagrama.) Si lo son, entonces el diagrama es rígido; de lo contrario, es simplemente un cuadrilátero no rígido.

Answer 2

La razón por la que te resulta difícil conciliar estas ideas es porque el diagrama se refiere a una noción física de rigidez, mientras que la página wiki que estás leyendo se centra en una noción geométrica de rigidez. (No encuentro que el artículo al que enlazaste esté particularmente bien escrito tampoco.)

Geometría

En geometría, en realidad no hablamos de formas rígidas, realmente hablamos de transformaciones rígidas. Las formas en geometría son simplemente conjuntos de puntos, no objetos físicos con resistencia a la flexión y al estiramiento. Están a merced de las transformaciones aplicadas a ellos.

Suponiendo que estemos trabajando en una geometría que tenga nociones de cómo medir ángulos y distancias:

Una transformación rígida conserva todas las distancias y medidas de ángulos (y dependiendo de tu gusto, también la orientación)

La idea es que no importa qué forma tengamos al principio, cualquier forma que dibujes en el plano en absoluto se verá igual después de aplicar una transformación rígida, excepto que su ubicación y situación podrían ser diferentes de lo que solían ser. (También podría ser su imagen reflejada, si has permitido transformaciones para invertir la orientación del plano.)

Muchas de esas formas cambiarían si elegimos una transformación no rígida, por ejemplo, la transformación dada por $x\mapsto x$ y $y\mapsto 2y$ en el plano cartesiano. Esto cambiaría un círculo en el origen en una elipse.

Si estás interesado en una geometría que no se base en la distancia, entonces puedes adoptar algunos axiomas de geometría que asuman nociones de congruencia de segmentos y ángulos. Las transformaciones rígidas del plano serían aquellas que no alteran la congruencia de segmentos ni la congruencia de ángulos.

Física

Ahora, hay una noción de rigidez en la realidad que tiene más que ver con su resistencia a cambiar de forma. Esto se llama rigidez estructural. Esto realmente no es el mismo animal que la rigidez de forma en geometría, aunque obviamente está relacionado.

En el diagrama que proporcionaste, parece que estamos asumiendo que los segmentos no cambian de longitud, pero que las articulaciones están en bisagras. Puedes aplicar fuerzas físicas a ambos y ver cómo se comportan. Uno clasificaría al triángulo como una forma rígida porque ninguno de sus longitudes de borde o ángulos cambiaría debido a la forma intrínseca del objeto. El cuadrado, por otro lado, no está limitado geométricamente a tener ángulos de 90 grados cuando se le aplica presión, por lo que puede convertirse rápidamente en un rombo.

Además, fácilmente podrías imaginar construir un objeto con segmentos que cambian de longitud y bisagras rígidas, de modo que un cuadrado se pudiera convertir en un rectángulo al estirarlo, pero no se pudiera empujar para convertirlo en un rombo. No creo que ese objeto se considere "rígido" tampoco.

Conclusión

Espero haber expresado un poco sobre la diferencia entre estos dos estudios.

No quiero decir que la noción física esté totalmente desligada de las matemáticas: seguramente la rigidez física se puede analizar con matemáticas. Simplemente que la página wiki sobre geometría no era donde querías estar si estás interesado en rigidez estructural.

Answer 3

Creo que la rigidez se usa de manera relativamente intuitiva aquí. Sin embargo, si quisiera ignorar cualquier pretensión de pureza geométrica y simplemente tratar de definir el concepto de una manera que funcione, lo haría de la siguiente manera: parece que uno necesita tener una noción de un borde ''inferior'', que consideramos fijo. Los demás deberían ser libres de moverse, y en particular queremos que las propiedades preservadas sean perímetro y área. Por lo tanto:

Una forma se llama rígida a lo largo de un borde $e$ si cualquier función continua $f$ que fija ese borde y preserva distancias geodésicas, de hecho también preserva distancias euclidianas (¿y área?).

Aquí, el concepto de distancias geodésicas es difícil de formalizar pero fácil de entender; simplemente es la distancia más corta entre dos puntos si se restringe a viajar a lo largo de los bordes de la forma. La distancia euclidiana es simplemente la longitud de la línea en el plano que conecta dos puntos.

Bajo esta definición $S_1$ es rígida a lo largo de $AB$: la propuesta de voltear a través de $AB$ no está permitida porque aunque las distancias geodésicas se han mantenido iguales, la distancia entre $C$ y $D$ ha disminuido

Más pensamientos:

• Dudo que la restricción continua sea necesaria, ¡pero las funciones no continuas son aterradoras y realmente no quería pensar en ellas! :)
• Tampoco estoy completamente convencido de que preservar el área sea necesario; esto puede ser realmente una condición estrictamente más débil que preservar geodésicas y euclidianas.
• Es posible que la rigidez a lo largo de cualquier $e$ implique rigidez a lo largo de cada $e$. Si no, es posible que desee definir las formas rígidas como aquellas que tienen rigidez a lo largo de cada $e$, dependiendo de sus motivaciones.

Answer 4

En dos mecanismos planos, si j es el número de uniones, L el número de eslabones, L = 2 j - 3. Esto lleva a armazones tan rígidos como un triángulo. Y en tres dimensiones, L = 3 j - 6.

Si se proporcionan más enlaces de los permitidos, partes del armazón diseñado comienzan a moverse como un mecanismo con grados de libertad adicionales.