Cuando se utiliza un divisor de voltaje en el análisis de circuitos

Question

Estoy tratando de encontrar el voltaje en R2 con un divisor de voltaje, este es el esquemático:

simular este circuito – Esquemático creado usando CircuitLab

pero no puedo, y no sé cómo aplicar el divisor de voltaje aquí. Lo que intenté hacer fue:

Primero convertí el Delta R2-R3-R4 a Y (estrella), porque el divisor de voltaje debe ser utilizado en un circuito en serie así que intenté convertir el delta a serie, pero eso solo funcionó para encontrar la Resistencia total.

simular este circuito

No sé qué valor tomará el R1 y R2 en la fórmula: $$ V_{out} = \frac{V_{in} * R_2}{R_1 +R_2} \\ $$

así que en este caso $$V_{out} = V_{R_2}$$ Estoy usando $$V_{in} = 10v$$, pero no puedo averiguar cuál debería ser la Resistencia total en este caso, quiero decir cuál es el valor de: $$R_1 +R_2$$

Encontré el Voltaje de R2 haciendo Análisis de Mallas. Pero no sé si es posible encontrar ese valor con el Divisor de Voltaje.

En el caso de que sea posible o no, ¿cuándo se debería usar el Divisor de Voltaje?

Gracias por cualquier pista.

Answer 1

Solo daré una pista aquí: piensa en el voltaje a través de R4 y cuánta corriente fluirá a través de ella. Si es necesario, quita R4 y calcula los voltajes en los puntos 4 y 6.

Si no fuera tan conveniente (por ejemplo, si todas las resistencias no tuvieran el mismo valor), puedes calcular Vth y Rth (Thevenin) para R2, R5 y R3, R6 (es decir, puntos 4 y 6). Luego, resuelve las cosas a partir de ahí.

Answer 2

Conceptos básicos y análisis del divisor de voltaje

Me di cuenta en un comentario posterior que realmente estabas tratando de entender cómo esto podría (potencialmente) hacerse utilizando la teoría del divisor de voltaje. Para empezar, déjame recordarte qué es realmente un divisor de voltaje:

Toma este divisor de voltaje resistivo de Wikipedia:

La ecuación común para encontrar la salida es: V_salida = R2 / (R1 + R2) * V_entrada

Pero lo que realmente se reduce a esto es: V_salida = R2 * I_R2

Por supuesto, en este circuito, la corriente a través de R1 y R2 es igual, por lo que encontrar el valor se hace fácilmente dividiendo el voltaje total por la corriente total: I = V_entrada / (R1 + R2)

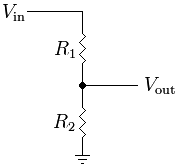
Debido a que R2 está ubicado entre V_salida y el suelo, el voltaje a través de R2 es igual a V_salida. Sin embargo, ¿qué sucedería si se colocara una tercera resistencia en paralelo con R2? Considera esta versión modificada de la imagen anterior:

La relación de corriente ha cambiado ahora. En este circuito, I_R1 = I_R2 + I_R3. Esto hace que la ecuación para la salida sea un poco más compleja: V_salida = (R2 || R3) / (R1 + (R2 || R3)) * V_entrada

Debido a que R2 y R3 están en paralelo: (R2 || R3) = (R2 * R3) / (R2 + R3)

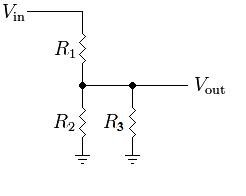
Pero el voltaje a través de R2 sigue siendo igual a V_salida. Agregar otra resistencia en serie cambia esto:

V_salida = ((R2 || R3) + R4) / (R1 + (R2 || R3) + R4) * Vin

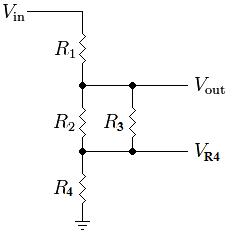
Ahora, el voltaje a través de R2 realmente es igual a V_salida - V_R4. Agregar más resistencias solo ampliará más la relación entre V_salida y V_R2. Agregar una resistencia en serie a R3 no cambia mucho las cosas:

V_salida = ((R2 || (R3 + R4)) + R5) / (R1 + (R2 || (R3 + R4)) + R5) * Vin

donde R2 está en paralelo con la combinación en serie de R3 y R4... Este sigue siendo un gran divisor de voltaje resistivo con resistencias en paralelo y en serie al azar. El voltaje a través de R2 es igual a V_salida - V_R5.

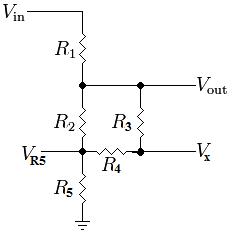
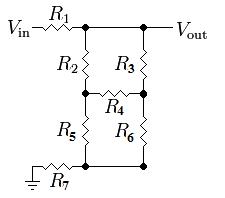
La verdadera complicación viene con la introducción de la mitad inferior del Puente de Wheatstone formado por las resistencias 2 a 6. Tu circuito en particular es muy simple porque todas las resistencias tienen el mismo valor (el puente está balanceado), pero es un poco más difícil formular ecuaciones para un circuito genérico que podría tener un voltaje a través de R4:

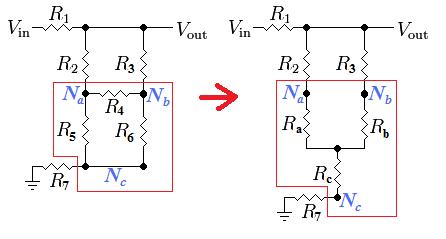
Si realmente quieres seguir utilizando relaciones resistivas básicas, el siguiente mejor paso es simplificar el circuito. Un método es realizar una Transformación Delta-Y, como mencionaste en la pregunta. Sin embargo, tiene mucho más sentido hacerlo en la mitad inferior o lado derecho del puente donde R2 no está involucrado. Por ejemplo, al convertir la mitad inferior del puente se obtiene:

Los nuevos valores de resistencia se encuentran como:

• Ra = R4 * R5 / (R4 + R5 + R6)
• Rb = R4 * R6 / (R4 + R5 + R6)
• Rc = R5 * R6 / (R4 + R5 + R6)

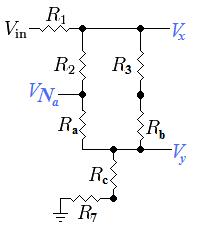
Pero esto aún no resuelve el problema porque necesitas conocer el voltaje a través de R2 que ahora es igual a V_salida - V_Na. Esto aún se puede resolver utilizando divisores de voltaje si utilizas un par de puntos distintos como salidas:

La solución final (el voltaje a través de R2) finalmente se puede encontrar utilizando una combinación de varios divisores de voltaje y las siguientes ecuaciones:

• Vx = [((R2 + Ra) || (R3 + Rb)) +Rc +R7] / [R1 + ((R2 + Ra) || (R3 + Rb)) +Rc +R7] * V_entrada
• Vy = (Rc + R7) / [R1 + ((R2 + Ra) || (R3 + Rb)) + Rc + R7] * V_entrada
• I_R2 = (Vx - Vy) / (R2 + Ra)
• V_R2 = R2 * I_R2

Dado que dijiste que ya encontraste la respuesta utilizando Análisis de Malla, procederé a colocar los valores que deberías obtener de las ecuaciones anteriores:

• Vx = 10V
• V7 = 6 & 2/3 V = 6.666...V
• I_R2 = 0.025A
• V_R2 = 2.5V

Así que es posible resolver el circuito utilizando solo divisores de voltaje, pero necesitábamos ayuda de una transformación de resistencia. Todas las técnicas básicas de análisis de circuitos se basan en la ley de Ohm: V = I*R, algunas de ellas simplemente tienen más sentido usarlas en ciertos momentos que otras.

Usando Análisis Nodal

Teniendo en cuenta que todas tus resistencias tienen el mismo valor, hay algunos trucos para reducir fácilmente todo el circuito, pero como eso es bastante irrealista en la vida real, creo que sería mejor enseñarte una herramienta de análisis real. Hay muchas formas de analizar un circuito, pero una de las más fáciles y mejores para muchos tipos de problemas es el Análisis Nodal. Es muy fácil de aprender.

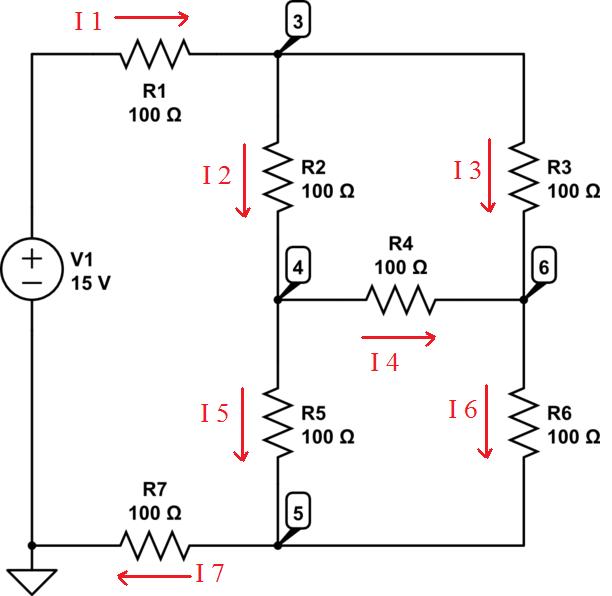
1) Según la ley de corrientes de Kirchhoff (LCK), la corriente que entra en un nodo (punto en el circuito) debe ser igual a la corriente que sale de ese mismo nodo. Así que divide el circuito en corrientes individuales fluyendo de un nodo a otro. La dirección del flujo de corriente depende completamente de ti, solo afectará la polaridad de la corriente resultante:

2) Forma relaciones entre las corrientes:

• I1 = I2 + I3
• I2 = I4 + I5
• I6 = I3 + I4
• I7 = I5 + I6
• I7 = I1

3) Expresa las corrientes como voltajes/resistencias

• I1 = (15V - V3) / R1
• I2 = (V3 - V4) / R2
• I3 = (V3 - V6) / R3
• I4 = (V4 - V6) / R4
• I5 = (V4 - V5) / R5
• I6 = (V6 - V5) / R6
• I7 = (V5 - 0V) / R7

4) Utilizando álgebra, combina y reduce las ecuaciones para encontrar los valores de los voltajes desconocidos. Para responder a tu pregunta específica, el voltaje a través de R2 sería V3 - V6 que es igual a R2 * I2.

Answer 3

Creo que el mejor enfoque es el que Clothier mencionó anteriormente. Pero deberías investigar más sobre el puente de Wheatstone ya que tus valores son los mismos. La conversión por Delta requiere más procesos y generalmente son tediosos. Si esos procesos siguen siendo tediosos, si fuera tú, usaría mallas, y obtendrías las siguientes ecuaciones:

$$15 = I_{1}(400)-I_{2}(100)-I_{3}(100)$$ $$0 = -I_{1}(100)+I_{2}(300)-I_{3}(100)$$ $$0 = -I_{1}(100)-I_{2}(100)+I_{3}(300)$$

O utiliza KCL, y luego:

$$v_{3}+v_{3}-v_{4}+v_{3}-v_{6}=15$$ $$v_{4}-v_{3}+v_{4}-v_{6}+v_{4}-v_{5}=0$$ $$3v_{6}-v_{3}-v_{4}-v_{5}=0$$ $$3v_{5}-v_{4}-v_{6}=0$$

Buena suerte con eso, en el futuro aprenderás mejores métodos como Thevenin, y simulaciones CAD.

---

Answer 4

En esta situación de circuito con todos los valores de R iguales, la evaluación es bastante simple. Primero note que V en 4 & 6 debe ser igual, por lo tanto R4 no tiene corriente y puede ser ignorada. La red R2-6 es básicamente otra resistencia equivalente de 100 ohmios. Eso hace que los voltajes en 3 & 5 sean 2/3 y 1/3 de la entrada V, es decir, 10 y 5 V respectivamente. Debido nuevamente a la igualdad de valores de resistencia, V a través de R2 debe ser la mitad de los 5V entre 3 & 5, o 2.5 voltios. Q.E.D.