En la prueba de la relación F=(9/5)C+32 (grados celsius a fahrenheit) asumimos que hay una relación lineal entre las dos escalas de temperatura: F=mC+b. Entonces necesitamos dos "puntos" para encontrar la ecuación de esa línea.
¿Cómo podemos explicar a un estudiante la forma muy específica (es decir, lineal) de la relación entre estas escalas de temperatura (o entre kelvin y grados celsius, rankine y grados fahrenheit, así como kelvin y rankine)?
Las escalas de temperatura definidas en el sistema de unidades SI están relacionadas con la unidad SI de temperatura, el kelvin, K.
En la ampliamente utilizada escala de temperatura Celsius, un grado Celsius es un intervalo de 1 K, y cero grados Celsius son 273.16 K.
Un intervalo de un grado Celsius corresponde a un intervalo de 1.8 grados Fahrenheit en la escala de temperatura Fahrenheit.
Por lo tanto, por definición la relación entre estas diferentes escalas de temperatura es lineal y la relación $F=\frac{9}{5}C+32$ es una consecuencia de esta definición.
Las constantes numéricas son un producto de la historia y del hecho de que el grado Celsius y el grado Fahrenheit son tan ampliamente utilizados.
El hecho de que, aunque un termómetro de mercurio en vidrio calibrado con 100 divisiones iguales entre el punto de hielo y el punto de vapor mida la temperatura de un objeto que es solo aproximadamente la misma que la medida utilizando un termómetro de alcohol en vidrio calibrado con 100 divisiones iguales entre el punto de hielo y el punto de vapor, significaba que una escala de temperatura necesitaba ser definida si se necesitaban medir temperaturas más precisas y reproducibles.
Otra forma de decir esto es que si la expansión térmica del mercurio (o alcohol o ...), la longitud de la columna líquida, se mide en relación a la escala de grado Celsius actualmente definida, la relación entre la expansión y la temperatura no es (exactamente) lineal pero para algunos propósitos puede considerarse aproximadamente lineal.
Para definir una escala de temperatura, necesitamos seguir tres pasos:
De hecho, tu pregunta está relacionada con el tercer paso. Digamos que estamos controlando el volumen de una porción de mercurio. Definimos que cuando está en equilibrio térmico con hielo derretido, el volumen $x_1$ de mercurio corresponde a $0^oC$. De manera similar, en el agua hirviendo definimos $x_2$ correspondiente a $100^oC. Luego elegimos interpolación lineal los puntos entre $x_1$ y $x_2. Tenemos algo como la figura debajo:
donde las temperaturas intermedias crecen linealmente con los valores intermedios entre $x_1$ y $x_2$.
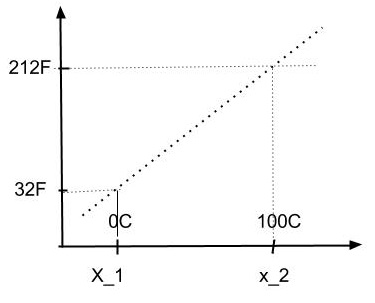
Por otro lado, consideremos nuevamente el volumen de mercurio y asociemos (por definición) los volúmenes $x_1$ y $x_2$, en el punto de fusión y ebullición, a las temperaturas $32F$ y $212F$. Finalmente decidimos usar interpolación lineal nuevamente. Por lo tanto, si graficamos la temperatura en Fahrenheit versus el volumen, obtenemos una línea recta (línea punteada), es decir,
Como podemos ver, la línea punteada, que es una línea recta, también proporciona una función entre la abscisa (C o volumen) y la ordenada (F). Es decir, las temperaturas en Fahrenheit y Celsius obedecen una relación lineal, $$T_F=A+BT_C.$$ Cabe destacar que las relaciones lineales son válidas entre dos escalas siempre y cuando ambas tengan interpolaciones lineales.
¿Por qué utilizas la expansión del mercurio como tu ejemplo? ¿No es la definición formal el volumen de una cantidad fija de un gas ideal? ¿Es el mercurio más accesible o relevante para los estudiantes?
@Qsigma El uso de mercurio (siempre y cuando utilice la misma sustancia para ambas escalas) es completamente arbitrario, ya que estoy hablando de temperatura empírica en lugar de temperatura termodinámica. Para ver la diferencia entre ambas, por favor consulta: ¿Cuál es la diferencia entre la temperatura termodinámica y la temperatura empírica?.
Creo que esta podría ser una posible forma de explicar por qué ambos son linealmente dependientes. Puede que no sea la mejor razón, pero definitivamente es una buena explicación.
Medimos las temperaturas basándonos en los termómetros que funcionan según el principio de la expansión de la materia. Dado que sabemos que el material utilizado en los termómetros se expande linealmente con la temperatura, podemos concluir que la temperatura en cualquier escala medida por el termómetro estará linealmente relacionada entre sí.
Si la linealidad (aproximada) de la temperatura fuera inexacta, entonces dos termómetros con los mismos dos puntos de calibración pero construidos de manera diferente registrarían diferentes temperaturas intermedias, especialmente cerca de la mitad entre los dos puntos de calibración. Dos construcciones diferentes podrían emplear materiales termo-sensibles distintos, por ejemplo mercurio y alcohol como se ha hecho históricamente.
Dado que esto no ocurre, la linealidad (aproximada) está establecida empíricamente.
Este podría ser un buen experimento para tu clase.
Dado que todas estas escalas podrían imprimirse en el mismo termómetro de mercurio, y debido a que cada escala está compuesta por unidades de igual longitud, una relación lineal entre las escalas es la única posible.
Esta relación lineal sigue siendo cierta incluso si no hay mercurio en el termómetro.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
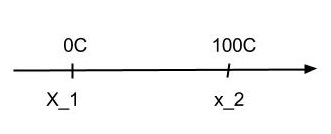
3 votos
¿Cuál es "la prueba de la relación $ F = (9/5) C + 32 $" ?
2 votos
¿Quién dice que son "lineales"? ¿Cómo sabes que el coeficiente de expansión del mercurio o el alcohol, o cualquier otra sustancia (cuando se expresa en unidades marcianas), no es altamente no lineal?