¿Cómo interpretar las unidades del producto punto o producto cruzado de dos vectores?

Question

Supongamos que tengo dos vectores $a=\left(1,2,3\right)$ y $b=\left(4,5,6\right)$, ambos en metros.

Si tomo su producto punto con la definición algebraica, obtengo lo siguiente:

$$a \cdot b = 1\mathrm m \cdot 4\mathrm m + 2\mathrm m \cdot 5\mathrm m + 3\mathrm m \cdot 6\mathrm m = 4\mathrm m^2 + 10\mathrm m^2 + 18\mathrm m^2 = 32 \mathrm m^2$$

El análisis dimensional me dice que esto está en metros cuadrados, si entiendo correctamente.

Sin embargo, al hacer el producto cruz, obtengo esto:

$$a \times b = \left[ \begin{array}{c} 2\mathrm m \cdot 6\mathrm m - 3\mathrm m \cdot 5\mathrm m\\ 3\mathrm m \cdot 4\mathrm m - 1\mathrm m \cdot 6\mathrm m\\ 1\mathrm m \cdot 5\mathrm m - 2\mathrm m \cdot 4\mathrm m\\ \end{array} \right] = \left[ \begin{array}{c} -3 \mathrm m^2\\ 6 \mathrm m^2\\ -3 \mathrm m^2\\ \end{array} \right] $$

Esto tampoco tiene sentido para mí.

No sé si estoy pensando en esto de la manera correcta, así que mi pregunta es la siguiente: al multiplicar por punto o cruz dos vectores, ¿cómo interpreto las unidades del resultado? Esta pregunta no se trata de interpretaciones geométricas.

Answer 1

Como ya ha señalado ACuriousMind has already noted, puedes interpretar geométricamente la longitud del producto cruzado de dos vectores como el área del paralelogramo (o como el doble del área del triángulo) que abarcan y (los valores absolutos) de sus componentes como las áreas de las proyecciones de ese paralelogramo en los planos coordenados.

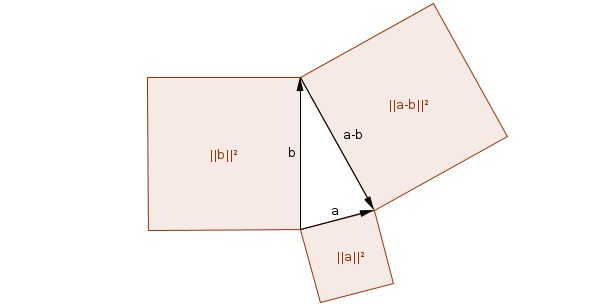
En cuanto al producto escalar de dos vectores, basado en el ley de los cosenos, puedes interpretarlo como la mitad de la diferencia entre la suma de sus cuadrados y el cuadrado de su diferencia:

$$\|\vec a - \vec b\|^2 = \|\vec a\|^2 + \|\vec b\|^2 - 2(\vec a \cdot \vec b).$$

En otras palabras, tomando los vectores como dos lados de un triángulo, el producto escalar mide (la mitad) de la cantidad por la que falla la ley de Pitágoras para este triángulo.

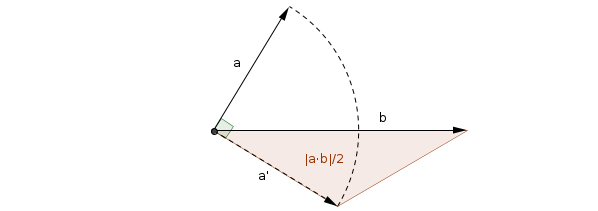
Otra forma de interpretar geométricamente (el valor absoluto del) producto escalar es como la mitad del área del triángulo formado al rotar uno de los vectores 90° en su plano común, y luego tomar los vectores resultantes como dos lados de un triángulo:

Esto se sigue de la bien conocida fórmula del producto escalar $\vec a \cdot \vec b = \|\vec a\| \|\vec b\| \cos \gamma$, donde $\gamma$ es el ángulo entre $\vec a$ y $\vec b$, de la fórmula del área del triángulo $T = \frac12 \|\vec a'\| \|\vec b\| \sin \gamma'$, donde $T$ es el área del triángulo formado por los vectores $\vec a'$ y $\vec b$ y $\gamma'$ es el ángulo entre ellos, y el hecho de que los ángulos $\gamma$ y $\gamma'$ son complementarios y por lo tanto $|\cos \gamma| = |\sin \gamma'|$.

Nota la similitud con el producto cruzado aquí. De hecho, siempre tenemos $\|\vec a \times \vec b\| = |\vec a' \cdot \vec b|$, donde $\vec a'$ es $\vec a$ rotado 90° en su plano común (o en cualquiera de los planos, si los hay).

---

Ps. Me di cuenta (después de publicar esta respuesta) de que preguntaste específicamente sobre las unidades de los productos y "no sobre interpretaciones geométricas." Sin embargo, estos ejemplos deberían al menos mostrar que tanto el producto escalar como el producto cruzado de dos vectores de longitud pueden, de hecho, ser interpretados significativamente como áreas, y por lo tanto, no debe ser sorprendente que, si los vectores originales tienen unidades, por ejemplo, de metros, entonces su producto se medirá en metros cuadrados.

Answer 2

La longitud del producto cruz de dos vectores es el área del paralelogramo que forman, por lo que los metros cuadrados son la unidad correcta y también tienen un significado geométrico real: realmente es un área. El componente $x$ es el área de la proyección del paralelogramo en el plano $y$-$z$, el componente $y$ es el área de la proyección en el plano $z$-$x$ y el componente $z$ es el área de la proyección en el plano $x$-$y.

La unidad del producto punto no tiene un significado realmente significativo. Por definición, es la longitud de la proyección del primer vector sobre el segundo multiplicada por la longitud del segundo (o viceversa), lo que no se corresponde directamente con ningún área. Por definición, tiene unidades de metros cuadrados, pero no veo una interpretación más profunda detrás de esto.

Answer 3

Me parece que siempre puedes factorizar las unidades de los componentes de un vector y reescribirlo como un vector sin dimensiones (físicamente) multiplicado por esas unidades. Luego, los productos punto y cruz funcionan en los vectores sin dimensiones y las unidades adjuntas simplemente se multiplican juntas como lo hacen en cualquier problema no vectorial.

En cuanto a la interpretación de las unidades resultantes, dependerá de si has construido algo que tenga un significado físico o no. Supongo que podrías tomar el producto cruz de dos vectores de fuerza, pero no creo que signifique nada (aunque estaría interesado en ver una interpretación si alguien puede pensar en una). Por supuesto, puedes tomar el producto cruz de un vector de posición y un vector de fuerza e interpretar el resultado como un torque.

Tu producto punto de dos vectores de posición tiene metros cuadrados como unidades porque corresponde a una longitud proyectada multiplicada por otra longitud. Y como otros ya han señalado, el producto cruz corresponde a un área.

Answer 4

El producto punto de dos longitudes no aparecerá en ninguna parte en la física, por eso la unidad no tiene significado.

Normalmente, tienes un producto punto en situaciones como $\cos(k\cdot r)$, donde el $\vec k$ se elige para dar un número significativo (fase) en el producto punto, tiene la unidad de 1/m. Vive en un espacio completamente diferente que los vectores de radio, pero de alguna manera están conectados en el sentido de que puedes comparar las direcciones de $\vec r$ y $\vec k, pueden ser paralelos, etc. Este "de alguna manera" necesita algo de matemáticas para escribirlo de manera más clara: en resumen, los k-s representan funcionales lineales en el espacio real...

O tienes un producto punto en algo como el cálculo del trabajo, donde la unidad también es significativa. Las matemáticas deberían ser similares aquí.

El producto cruzado se explica en la otra respuesta.

Answer 5

Un producto punto, al igual que un producto regular, producirá una cantidad diferente, generalmente con una unidad diferente. Eso no es sorprendente, la multiplicación siempre hace eso (ese es el punto de las unidades, forman un grupo multiplicativo).

Considere la versión de escuela primaria del trabajo=fuerza*desplazamiento. Lo escribe como $W=Fx$ (como "escalares"), probablemente no objetaría a eso. Bueno, resulta que solo la fuerza a lo largo del desplazamiento cuenta como trabajo, y en general, necesitas escribir $W={\bf F\cdot x}$. Así que realmente nada cambió, excepto que ahora se tienen en cuenta las direcciones (el producto punto solo multiplica partes de los vectores que son paralelas entre sí). La unidad resultante es, por supuesto, el Julio (o alguna otra unidad de energía), igual que en el caso escalar.

Para un producto cruz, esencialmente es lo mismo. Considere el torque. Tienes $\bf M= r\times F$. El torque es una cantidad diferente que la distancia o la fuerza. Eso habría sido el caso incluso sin la naturaleza vectorial de las cantidades.

Sin embargo, hay algo más sutil que eso. El producto cruz no produce un verdadero vector, no cuando lo examinas muy de cerca. La "sensación" de los componentes del producto vectorial tiene un área orientada alrededor de ella ... así que no es "cuánto de esto y esto tenemos en alguna dirección" sino "cuánto de esto y esto atraviesa un área que apunta en alguna dirección". Llamamos a esos pseudovectores (vectores axiales). Además de tener esta "sensación" de circularidad alrededor de alguna dirección (mira el torque - se retuerce alrededor de un eje), también tiene diferentes propiedades de simetría. Si inviertes todos los vectores en la ecuación (voltea la flecha), el producto cruz no voltea la flecha (porque en realidad no es una flecha, es un eje).

Este punto "sutil" no es necesario para entender la parte sobre las unidades (eso es solo porque un producto siempre crea una cantidad diferente), pero lo incluyo por completitud. Las cantidades físicas son más que solo números con unidades. Hay un significado y comportamiento detrás. Solo recuerda que el trabajo y el torque tienen las mismas unidades, pero uno es un escalar y el otro es un pseudovector.