Cauchy Valor principal de la integral con punto indefinido

Question

Esta es una pregunta de seguimiento de mi post en Stack Overflow . Quiero integrar (analítica o numéricamente):

$I=\displaystyle\int_{-\infty}^{\infty}\dfrac{1}{(z+1)^2+4} \dfrac{1}{\exp(-z)-1} dz$

usando MATLAB, pero me dice que la integral puede no existir - la integral es indefinida en $z=0$ . El valor principal de Cauchy tampoco parece existir, así que ¿qué nos dice esto sobre la integral? ¿Significa que no podemos evaluar $I$ (numéricamente o de otro modo)?

Answer 1

Si amplía $\frac{1}{\exp(-z)-1}$ en una serie de Taylor alrededor de $z=0$ , te das cuenta de que $$ \frac{1}{\exp(-z)-1}\approx -\frac{1}{z}-\frac{1}{2}-\frac{z}{12}+\ldots $$ por lo que la función tiene efectivamente una singularidad no integrable en $z=0$ . Una forma de asignar un resultado finito a su integral es restar y volver a sumar la parte singular a su integral como $$ \int_{-\infty}^{\infty}\dfrac{1}{(z+1)^2+4} \left[\dfrac{1}{\exp(-z)-1}+\frac{1}{z}-\frac{1}{z}\right]= $$ $$ \int_{-\infty}^{\infty}\dfrac{1}{(z+1)^2+4} \left[\dfrac{1}{\exp(-z)-1}+\frac{1}{z}\right]-\mathcal{P}\int_{-\infty}^{\infty}\dfrac{1}{(z+1)^2+4} \frac{1}{z}\ , $$ donde $\mathcal{P}$ es la parte principal de Cauchy. El resultado final es $-0.383448...$ (Comprobado y de acuerdo con la respuesta de Claude a continuación).

Answer 2

Como la antiderivada no existe, sólo se pueden utilizar métodos numéricos.

Como Ander Biguri respondió a su pregunta anterior, intenté calcular, con la mayor precisión posible $$I_k=\int_{-\infty }^{-10^{-k} } \frac{dz}{\left(e^{-z}-1\right) \left((z+1)^2+4\right)}+\int_{10^{-k} }^{\infty } \frac{dz}{\left(e^{-z}-1\right) \left((z+1)^2+4\right)}$$ Los resultados son los siguientes $$I_1=-0.3794424331$$ $$I_2=-0.3830481054$$ $$I_3=-0.3834081111$$ $$I_4=-0.3834441111$$ $$I_5=-0.3834477111$$ $$I_6=-0.3834480711$$ $$I_7=-0.3834481071$$ $$I_8=-0.3834481107$$ $$I_9=-0.3834481110$$

Editar

Después de la respuesta de Pierpaolo Vivo, es curioso observar que lo que escribió da $$I=-0.6976073764+\frac \pi {10}$$ ¿Quién esperaba $\pi$ para estar aquí?

Answer 3

Otra forma hábil de tratar esto que también aprovecha la observación de Pierpaolo es cancelar la parte singular a través de un incluso transformación:

$$\int_{-\infty}^\infty f(x)\mathrm dx=\int_{-\infty}^\infty \frac{f(x)+f(-x)}{2}\mathrm dx$$

En este caso, debe considerar la integral

$$\int_{-\infty }^\infty \frac{(z+2-(z-2)\exp z)\frac{z}{\exp z-1}-5}{2\left(z^4+6z^2+25\right)} \mathrm dz$$

donde el integrando tiene una singularidad removible en $z=0$ . Si tu rutina de cuadratura no muestrea exactamente en ese punto, deberías estar bien. (Como alternativa, hay formas para manejar el factor $\frac{z}{\exp z-1}$ .) Mathematica en particular, se obtiene fácilmente el resultado $-0.38344811106405680779$ .

Answer 4

Hice un análisis (no riguroso) basado en los residuos en el plano Im[z]>0.

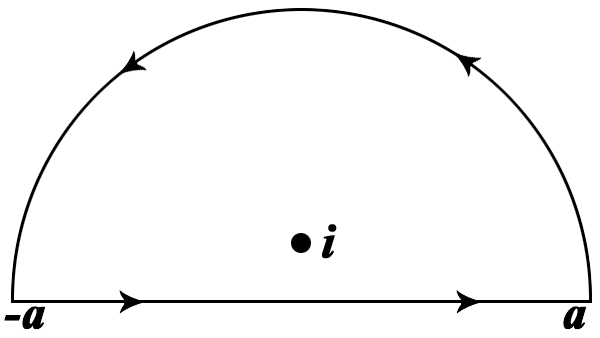
Dejemos que $C$ sea el contorno que va desde $-a$ a $a$ (en línea recta sobre el eje real), y de vuelta sobre el semicírculo $|z|=a$ con $Im[z]\ge0$ Véase la imagen (tomada de Wikipedia) que aparece a continuación.

Dentro de este contorno, el integrando es analítico, excepto por un número finito de polos: el polo en $z=-1+2i$ debido al primer factor, y los polos en $z=2\pi n$ para $n=1,2,...,N$ debido al segundo factor. Aquí, $N$ es el mayor número entero tal que $2\pi N<a$ . También hay un polo exactamente en el contorno, en $z=0$ .

Según el teorema del residuo, la integral de contorno sobre C puede calcularse sumando los residuos de estos polos y multiplicándolos por $2\pi i$ . (No olvides, aquí y después, que el poste de $z=0$ sólo cuenta la mitad, porque el contorno lo atraviesa).

Ahora, dejemos que $a$ ir al infinito. Esto también significa que $N$ se irá al infinito. Si la contribución de la parte semicircular del contorno llega a cero, todo lo que queda es $I$ . (No tengo ninguna prueba de que la contribución sea nula. De hecho, tengo algunas dudas por $z\rightarrow i\infty$ ... Pero como el resultado posterior parece coincidir con los valores numéricos, ignoro esto, y supongo que se podría hacer con rigor restringiendo $R$ a valores tales que el contorno cae entre los polos y no sobre los polos).

Los polos en $z=2n\pi i$ generan una suma infinita, que converge. Puse esta suma en Wolfram Alpha, y esto mostró que la suma se puede escribir con funciones digamma. El polo en $z=-1+2i$ da un término más. En total, el resultado es:

$$I=-\frac{\pi}{5} i -\frac{i}{4}\left(\psi\left(1-\frac{(1+\frac{i}{2})}{\pi}\right)-\psi\left(1+\frac{(1-\frac{i}{2})}{\pi}\right)\right)-\frac{\pi}{2-2e^{1-2i}}.$$

donde $\psi$ es la función digamma. Se puede simplificar un poco más utilizando la relación de recurrencia $\psi(1+x)=\psi(x)+1/x$ y la fórmula de reflexión $\psi(1-x)=\pi\cot(\pi x)+\psi(x)$ .

Aunque la expresión para $I$ tiene la unidad imaginaria $i$ en él, es un número real.

Según wolframio alfa%2Fpi)-digamma(1%2B((1-i%2F2))%2Fpi))-pi%2F(2-2e%5E(1-2i))) se evalúa en -0,383448111064056808053521526581710702474772465557555272482. Esto se corresponde con las otras respuestas encontradas numéricamente aquí, por lo que confío en que este análisis se pueda hacer con rigor.

Intenté si los términos del digamma podían ser simplificados, ya que parece haber una simetría agradable en él, pero no pude ver cómo hacerlo realmente más simple.