Klein j-invariante tiene la estructura que se parece a parecerse a los de Ford círculos:
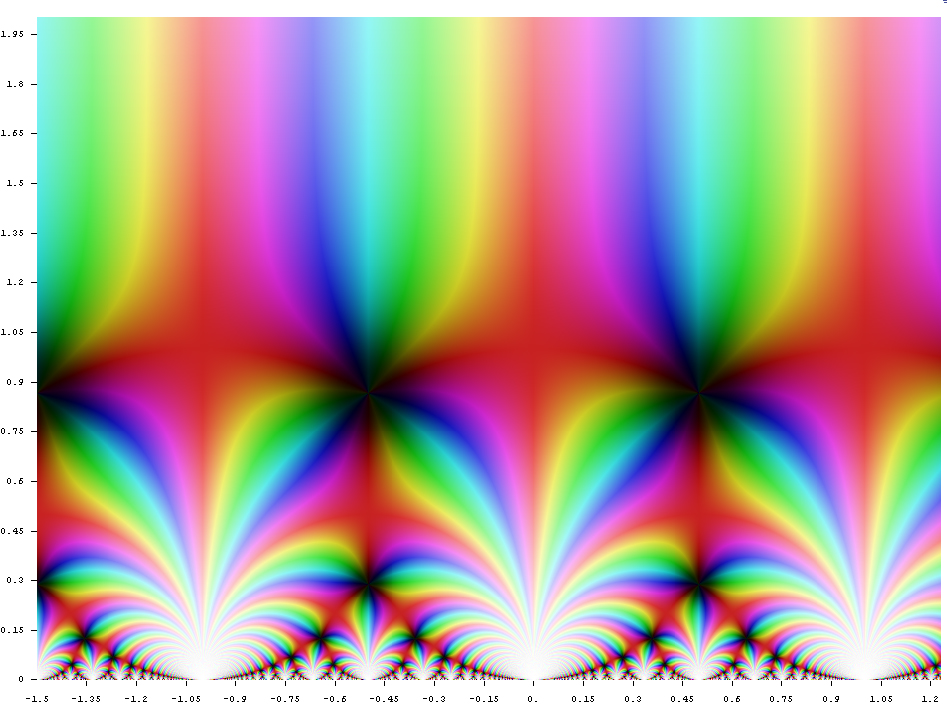
El último show en la teoría de los números (fracciones continuas, Rademacher la expansión de p(n), etc.)
Alguien puede explicar la conexión?
Klein j-invariante tiene la estructura que se parece a parecerse a los de Ford círculos:

El último show en la teoría de los números (fracciones continuas, Rademacher la expansión de p(n), etc.)
Alguien puede explicar la conexión?
Ford círculos son la órbita de un horocycle bajo la acción de la modulares grupo Γ en la mitad superior del plano de h (ver, por ejemplo, esta entrada de la SBS). Las formas modulares de peso cero (de los cuales el j-invariante es un ejemplo) son plenamente SL2(Z)-invariante. Así que los plazos de j (que representa el cociente H/Γ) mosaico del plano hiperbólico (de los cuales, h es un modelo) de acuerdo a la misma simetría , como el Ford círculo de ordenamiento en teselas.
El Ford círculos son también un diagrama de PSL2Z. Una buena discusión es en La Sensual Forma Cuadrática por John H. Conway. Los círculos son horocycles en lugar de geodesics. Comparar http://en.wikipedia.org/wiki/Modular_group#Tessellation_of_the_hyperbolic_plane
Sólo para comenzar la parte que realmente saben, si tienen un binario forma cuadrática f(x,y)=ax2+bxy+cy2, which we abbreviate as ⟨a,b,c⟩, the traditional question is the possible primitively represented values of f, that is f(p,q) with gcd Sin embargo, esto realmente no es muy diferente de encontrar la clase de equivalencia de forma. La equivalencia es, probablemente, ilustra mejor con el de Hesse de la matriz de segundas derivadas parciales H =\left( \begin{array}{cc} 2a & b \\ b & 2c \end{array} \right).
Tome una matriz en la SL_2 \mathbb Z y se multiplican con la matriz de la derecha de H y su transposición a la izquierda, como en \left( \begin{array}{cc} \alpha & \gamma \\ \beta & \delta \end{array} \right) \left( \begin{array}{cc} 2a & b \\ b & 2c \end{array} \right) \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \; = \; \left( \begin{array}{cc} 2A & B \\ B & 2C \end{array} \right). El resultado es la matriz Hessiana de una nueva forma de \langle A,B,C \rangle. La relación que primitivamente representado los valores es que f(\alpha, \gamma) = A.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.