Tiendo a escuchar que normalmente 3 mayores valores propios son los más importantes, mientras que aquellos que están cerca de cero ruido
Usted puede probar. Ver el artículo relacionado en este post para más detalles. De nuevo, si su trato con financial times serie puedes querer corregir leptokurticity primera (es decir, considerar la serie de garch-retornos ajustados, no la vuelve primas).
Yo he visto un par de artículos de investigación la investigación de cómo se produce naturalmente autovalor distribuciones difieren de los calculados a partir de azar matrices de correlación (de nuevo, distinguising el ruido de la señal).
Edward:> por lo general, uno podría hacerlo de la otra manera alrededor: mira multivariante de la distribución de autovalores (de matrices de correlación) de la aplicación que desea. Una vez identificado un candidato creíble para la distribución de autovalores, que debería ser relativamente fácil generar a partir de ellos.
El mejor procedimiento sobre cómo identificar multivariante de la distribución de sus valores propios, depende de la cantidad de recursos que desee considerar simultáneamente (es decir, ¿cuáles son las dimensiones de la matriz de correlación). Hay un truco si $p\leq 10$ ($p$ el número de activos).
Editar (comentarios por Shabbychef)
cuatro paso el procedimiento:
- Supongamos que usted ha $j=1,...,J$ sub-muestras de datos multivariantes. Usted necesita un estimador de la varianza-covarianza de la matriz $\tilde{C}_j$ para cada sub-muestra de $j$ ( puedes utilizar el estimador clásico o una alternativa robusta, tales como el rápido MCD, que es bien implementado en matlab, SAS, S,R,...). Como de costumbre, si su trato con el financial times, la serie habría que considerar la serie de garch-retornos ajustados, no vuelve primas.
- Para cada sub-muestra $j$, calcular $\tilde{\Lambda}_j=$ $\log(\tilde{\lambda}_1^j)$ ,..., $\log(\tilde{\lambda}_p^j)$ , los eigen valores de $\tilde{C}_j$.
- Calcular $CV(\tilde{\Lambda})$, el casco convexo de la $J \times p$ matriz cuya j-ésima es $\tilde{\Lambda}_j$ (de nuevo, esto está muy bien implementado en Matlab, R,...).
- Dibujar puntos al azar dentro de $CV(\tilde{\Lambda})$ (esta hecho por dar peso $w_i$ a cada uno de los bordes de $CV(\tilde{\Lambda})$ donde $w_i=\frac{\gamma_i}{\sum_{i=1}^{p}\gamma_i}$ donde $\gamma_i$ es un sorteo de una unidad de distribución exponencial (más detalles aquí).
Una limitación es que rápido cálculo del casco convexo de una serie de puntos que se vuelve extremadamente lento cuando el número de dimensiones es mayor que 10. $J\geq2$
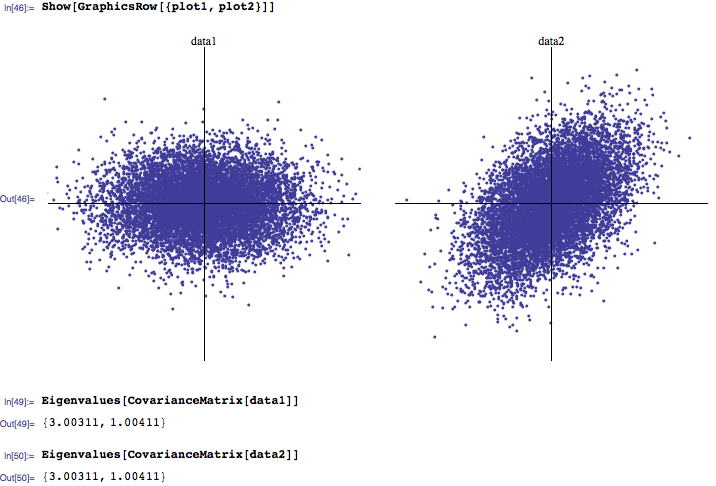El primer conjunto de datos se generó a partir de Gauss con matriz de covarianza $\left(\matrix{3&0\\0&1}\right)$ segundo conjunto de datos es el primer conjunto de datos girado por $\pi/4$
