Si $AM$, $BN$, $CP$ son cuerdas paralelas en la circunferencia circunscrita al triángulo equilátero $ABC$, entonces $\triangle MNP$ también es equilátero

Question

Aquí hay un problema interesante, y su resultado, que deseo compartir con la comunidad matemática aquí en Math SE.

El problema anterior tiene dos métodos.

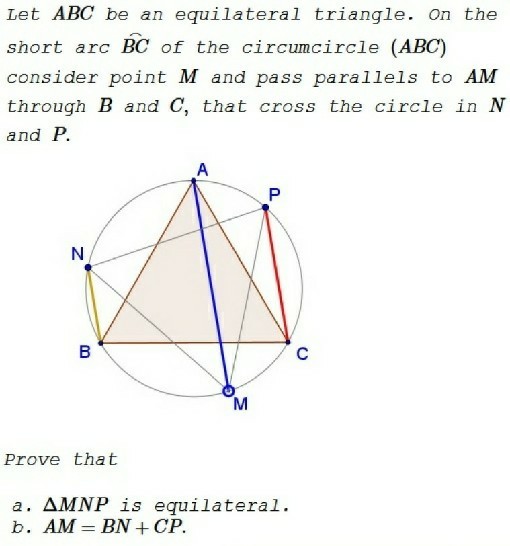
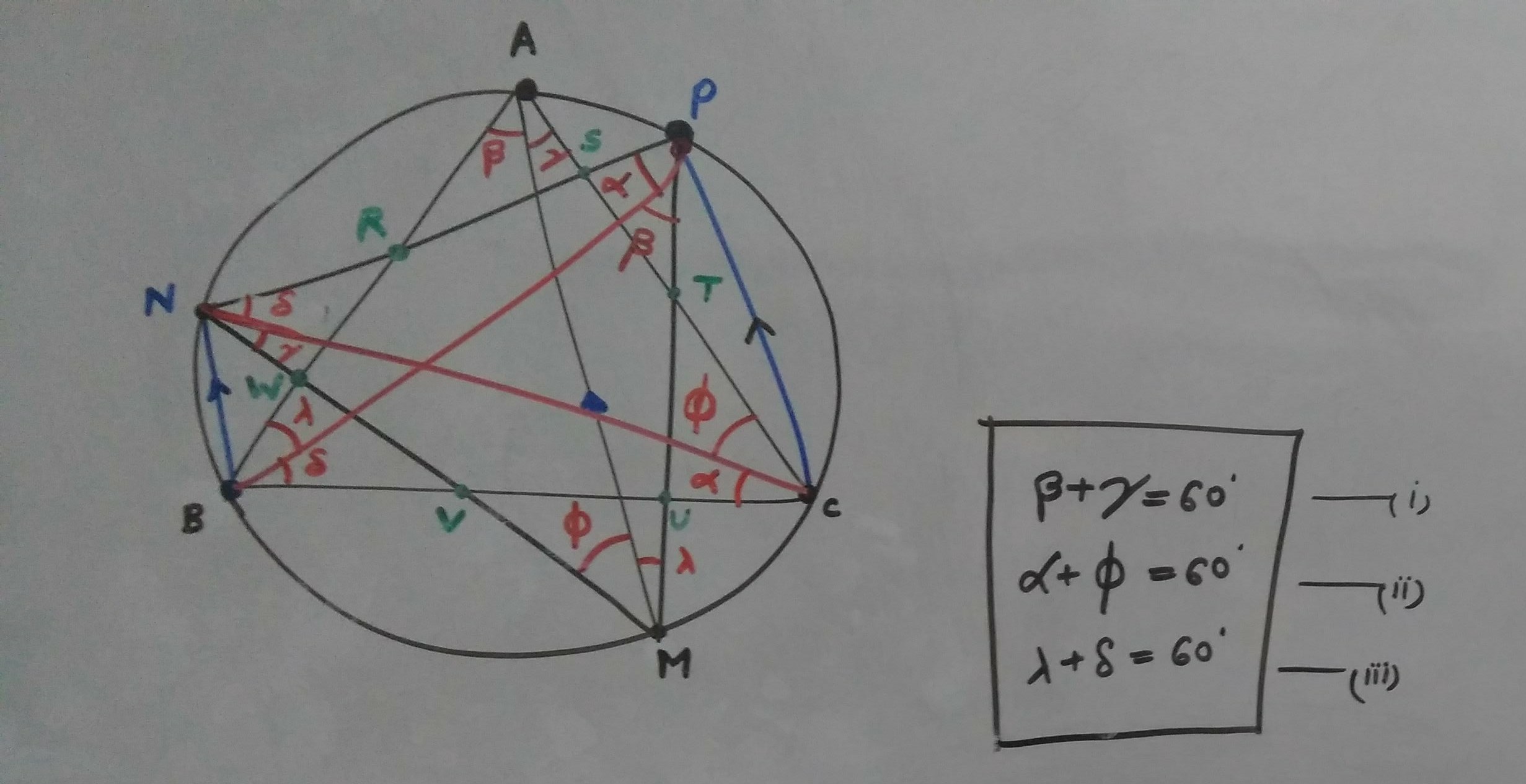
1. Geometría pura. Un poco de persecución de ángulos y resultados estándar de los círculos nos ayudan a llegar al resultado deseado: MNP es equilátero.

Uní BP y CN con fines de persecución de ángulos.

(Nótese que si M es el punto medio del arco BC, entonces la figura formada es una estrella, con 8 triángulos equiláteros)

2. Esto se puede resolver bellamente usando números complejos. Se puede asumir que los vértices del triángulo son 1, W, W2 en un círculo unitario centrado en el origen.

Necesitamos demostrar que el nuevo triángulo equilátero es esencialmente una rotación del original, alrededor de un eje que pasa por el centro de su circunferencia perpendicular a su plano.

No he publicado la solución, espero que ustedes, miembros de Math SE, intenten el problema y publiquen sus soluciones e ideas en la sección de respuestas.

Se aceptan más métodos (aparte de la geometría y los números complejos). Me gustaría saber más sobre por qué este resultado es interesante en sí mismo, y qué otras deducciones se pueden hacer a partir de él.

Answer 1

Una prueba geométrica para la parte a.

Del OP:

Necesitamos demostrar que el nuevo triángulo equilátero es esencialmente una rotación del original, alrededor de un eje que pasa por el centro de su circumcirculo y es perpendicular a su plano.

Creo que es más fácil pensarlo como una reflexión. En el diagrama abajo

• $GH$ es el diámetro del circumcírculo que es perpendicular a $AM$.
• Se da que $BN$ y $CP$ son paralelos a $AM$.
• Por lo tanto, los puntos $M, N, P$ son reflexiones de los puntos $A, B, C$ respectivamente en la línea $GH$.
• Por lo tanto, $\triangle MNP$ es una reflexión de $\triangle ABC$ a través de la línea $GH$.

Editar, para agregar la parte b.

Por medio de la simetría reflectante alrededor de $GH$ y la simetría rotacional de los triángulos equiláteros, podemos notar que $AP=BN=CM$, y que $AN=BM=CP$. De esto podemos trazar un sistema de líneas paralelas para mostrar que $AM=BN+CP$.

Answer 2

Pista geométrica: los trapezoides cíclicos $APCM, AMBN$ deben ser isósceles, por lo que los arcos $\overparen{AP}=\overparen{CM}$ y $\overparen{BM}=\overparen{AN}\,$. Dado que $\,\overparen{AB}=\overparen{BC}\,$, lo último implica $\overparen{BN}=\overparen{AB}-\overparen{AN}=\overparen{BC}-\overparen{BM}=\overparen{CM}\,$, por lo que al final $\overparen{AP}=\overparen{CM}=\overparen{BN}\,$ y, por lo tanto, el triángulo $\triangle PNM$ es $\triangle ABC$ rotado por $\overparen{AP}$.

---

En cuanto al punto b, escribiendo el teorema de Pitágoras dos veces:

• $APCM\,$: $\;AC^2=AP^2 + AM \cdot CP$

• $AMBN\,$: $\;AB^2=AN^2 + AM \cdot BN$

Restando lo anterior y utilizando que $AC=AB, AP=BN, CP=AN\,$:

$$ 0 = BN^2-CP^2+AM\cdot(CP-BN) = (BN-CP)\cdot(BN+CP-AM) $$

Se sigue que $\,BN+CP-AM=0 \iff AM = BN+CP\,$.  (Rigurosamente, el caso $\,BN=CP\,$ tendría que considerarse por separado, o podría derivarse por continuidad).

Answer 3

Permítanme agregar una respuesta para (b), asumiendo que (a) está probado...

Dibuja una línea a través de $P$ paralela a $CM$, y que intersecte $AM$ en $Q$. $PQMC$ es un paralelogramo, entonces $CP$=$QM$.

Por otro lado, es fácil ver que $\triangle APQ$ es equilátero, ya que sus ángulos son de $60^\circ$ ($\angle A$ es periférico sobre el arco $\overparen{PM}$ y $\angle Q=\angle CMA$ es periférico sobre el arco $\overparen{AC}$). Así que, $AQ$=$AP$=$BN$.

Finalmente, $AM=AQ+QM=BN+CP$ como se afirmó.

Answer 4

Esto se puede resolver de manera hermosa usando números complejos. Se puede suponer que los vértices del ∆ son 1, W, W2 en un círculo unitario centrado en el origen.

Aquí hay un intento de demostrarlo usando números complejos.

Estoy tratando de demostrarlo al revés. Sean C, A, B $1$, $\omega$, $\omega^2$ y M $e^{i\theta}$.

Si $\Delta$MPN es un triángulo equilátero, entonces AM||PC lo cual implica

AM=$e^{i\theta}-\omega$

OP=OM$\times \omega$

PC=$e^{i\theta}\omega-1$

Tenemos que probar que AM=$\lambda$PC, para algún escalar $\lambda$

@schrodinger_16, ¿me puedes ayudar a continuar?