Dibujando un gráfico que es plano, pero luego picos

Question

Intento crear una función que haga un gráfico como este:

 |
|
|           -
|          - -
|         -   -
|        -     -
|--------       --------
|-----------------------
 

Estoy atrapado con:$1/((x-1.5)^2)$

¿Alguna ayuda?

Answer 1

Algunas veces, tales funciones se llaman funciones triangulares o de carpa .

El ejemplo más básico centrado en$0$ se ve así: $$f (x) = \begin{cases} 1- |x|, & \text{if }|x|<1\\ 0, & \text{ else} \end {cases}$$

Answer 2

Puedes hacer$y=e^{-x^2}$. No es exactamente plano en los lados, pero prácticamente lo es. Puede editar el$e$,$2$, el coeficiente o el denominador para cambiar la forma (y traducirla donde lo necesite).

Como sugiere el comentario a continuación, es una Curva Gaussiana.

Answer 3

Si usted quiere que su función sea tanto suave y cero en todas partes fuera de un intervalo finito, lo que necesitas es una protuberancia de la función. Un ejemplo clásico es $$f(x) = \begin{cases} e^{-1/(1-x^2)} & \text{for } -1 \le x \le 1 \\ 0 & \text{otherwise}, \end{cases}$$ , que se parece a esto:

$\hspace{70px}$
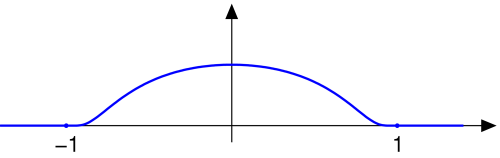
^{(Imagen de Wikimedia Commons, creado y publicado en el dominio público por Oleg Alexandrov.)}

Answer 4

La función$1/(x-1.5)^2$ que apuntó no podría tener esa forma. Pero hacer algunos cambios puede hacer que tenga esa forma de deseo. Es$$f(x)=\frac{1}{(x^2+1.5)^2}