Cuál es el propósito de la normalización de filas

Question

Entiendo el razonamiento detrás de la normalización de columnas, ya que hace que las características tengan el mismo peso, incluso si no se miden en la misma escala - sin embargo, a menudo en la literatura de vecinos más cercanos, tanto las columnas como las filas se normalizan. ¿Para qué se normalizan las filas? Específicamente, ¿cómo afecta el resultado de la normalización de filas a la similitud/distancia entre los vectores de fila?

Answer 1

Hay algunas razones específicas del campo para realizar la normalización de filas. En el análisis de texto, es bastante común representar un texto con el histograma de las palabras que contiene. Comenzando desde el conteo de palabras para cada línea, la estandarización cruda lo convierte en un histograma.

Y la razón computacional. Si estás trabajando con una matriz dispersa, no puedes centrar y escalar los datos columna por columna fácilmente. Si la insertas en una matriz densa, los datos pueden volverse demasiado grandes para caber en la memoria. Sin embargo, escalar fila por fila no afecta la cantidad total de memoria necesaria.

Answer 2

Este es un hilo relativamente antiguo, pero recientemente encontré este problema en mi trabajo y tropecé con esta discusión. La pregunta ha sido respondida, pero siento que el peligro de normalizar las filas cuando no es la unidad de análisis (ver respuesta de @DJohnson arriba) no ha sido abordado.

El punto principal es que normalizar las filas puede ser perjudicial para cualquier análisis posterior, como el de vecino más cercano o k-means. Para simplificar, mantendré la respuesta específica de centrar las filas en la media.

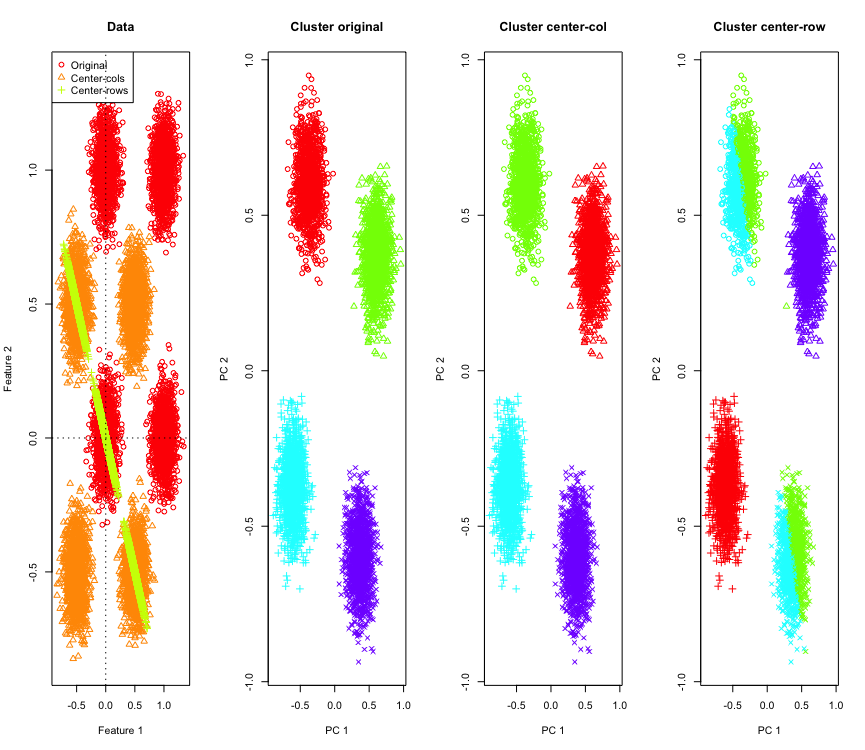
Para ilustrarlo, utilizaré datos gaussianos simulados en las esquinas de un hipercubo. Afortunadamente en R hay una función conveniente para eso (el código está al final de la respuesta). En el caso 2D es directo que los datos centrados en la media de las filas caerán en una línea que pasa por el origen a 135 grados. Los datos simulados son luego agrupados usando k-means con el número correcto de grupos. Los datos y los resultados del agrupamiento (visualizados en 2D utilizando PCA en los datos originales) se ven así (los ejes para el gráfico más a la izquierda son diferentes). Las formas diferentes de los puntos en los gráficos de agrupamiento se refieren a la asignación de grupos verdadera y los colores son el resultado del agrupamiento k-means.

Los grupos de la parte superior izquierda y la parte inferior derecha se dividen por la mitad cuando los datos se centran en la media de las filas. Por lo tanto, las distancias después de centrar en la media de las filas se distorsionan y no son muy significativas (al menos según el conocimiento de los datos).

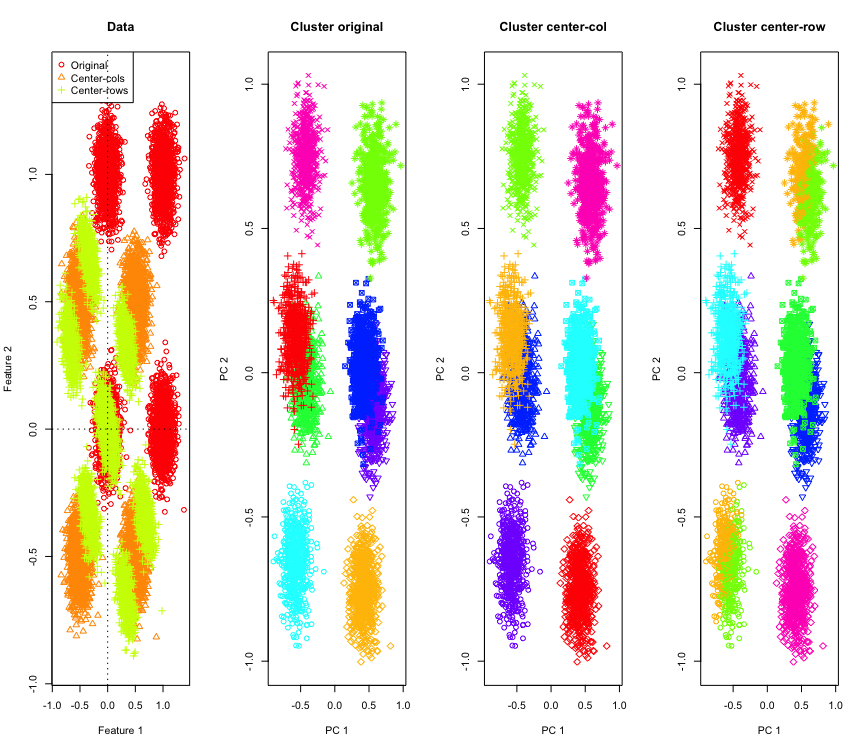
No es tan sorprendente en 2D, ¿qué sucede si usamos más dimensiones? Así es como se ve con datos 3D. La solución de agrupamiento después de centrar en la media de las filas es "mala".

Y similar con datos 4D (ahora no se muestra por brevedad).

¿Por qué está sucediendo esto? Centrar en la media de las filas empuja los datos hacia un espacio donde algunas características se acercan más de lo que lo hacen de otra manera. Esto debería reflejarse en la correlación entre las características. Veamos eso (primero en los datos originales y luego en los datos centrados en la media de las filas para los casos 2D y 3D).

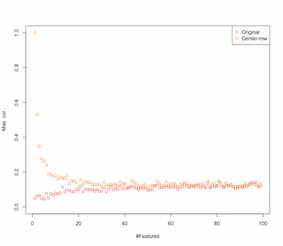
[,1] [,2] [1,] 1.000 -0.001 [2,] -0.001 1.000 [,1] [,2] [1,] 1 -1 [2,] -1 1 [,1] [,2] [,3] [1,] 1.000 -0.001 0.002 [2,] -0.001 1.000 0.003 [3,] 0.002 0.003 1.000 [,1] [,2] [,3] [1,] 1.000 -0.504 -0.501 [2,] -0.504 1.000 -0.495 [3,] -0.501 -0.495 1.000 Entonces parece que centrar en la media de las filas está introduciendo correlaciones entre las características. ¿Cómo se ve afectado esto por el número de características? Podemos hacer una simulación simple para averiguarlo. El resultado de la simulación se muestra a continuación (nuevamente el código al final).

Entonces, a medida que aumenta el número de características, el efecto de centrar en la media de las filas parece disminuir, al menos en cuanto a las correlaciones introducidas. Pero simplemente usamos datos aleatorios uniformemente distribuidos para esta simulación (como es común cuando se estudia la maldición de la dimensionalidad).

¿Qué sucede cuando usamos datos reales? Como muchas veces la dimensionalidad intrínseca de los datos es menor la maldición podría no aplicarse. En tal caso, supondría que centrar en la media de las filas podría ser una elección "mala", como se muestra arriba. Por supuesto, se necesita un análisis más riguroso para hacer afirmaciones definitivas.

Código para la simulación de agrupamiento

palette(rainbow(10))
set.seed(1024)
require(mlbench)
N <- 5000
for(D in 2:4) {
X <- mlbench.hypercube(N, d=D)
sh <- as.numeric(X$classes)
K <- length(unique(sh))
X <- X$x

Xc <- sweep(X,2,apply(X,2,mean),"-")
Xr <- sweep(X,1,apply(X,1,mean),"-")

show(round(cor(X),3))
show(round(cor(Xr),3))

par(mfrow=c(1,1))

k <- kmeans(X,K,iter.max = 1000, nstart = 10)
kc <- kmeans(Xc,K,iter.max = 1000, nstart = 10)
kr <- kmeans(Xr,K,iter.max = 1000, nstart = 10)
pc <- prcomp(X)
par(mfrow=c(1,4))

lim <- c(min(min(X),min(Xr),min(Xc)), max(max(X),max(Xr),max(Xc)))
plot(X[,1], X[,2], xlim=lim, ylim=lim, xlab="Característica 1", ylab="Característica 2",main="Datos",col=1,pch=1)
points(Xc[,1], Xc[,2], col=2,pch=2)
points(Xr[,1], Xr[,2], col=3,pch=3)
legend("topleft",legend=c("Original","Centro-columnas","Centro-filas"),col=c(1,2,3),pch=c(1,2,3))
abline(h=0,v=0,lty=3)

plot(pc$x[,1], pc$x[,2], col=rainbow(K)[k$cluster], xlab="PC 1", ylab="PC 2", main="Agrupamiento original", pch=sh)
plot(pc$x[,1], pc$x[,2], col=rainbow(K)[kc$cluster], xlab="PC 1", ylab="PC 2", main="Agrupamiento centro-columna", pch=sh)
plot(pc$x[,1], pc$x[,2], col=rainbow(K)[kr$cluster], xlab="PC 1", ylab="PC 2", main="Agrupamiento centro-fila", pch=sh)
}

Código para simulación de aumento de características

set.seed(2048)
N <- 1000
Cmax <- c()
Crmax <- c()
for(D in 2:100) {
X <- matrix(runif(N*D), nrow=N)    
C <- abs(cor(X))
diag(C) <- NA
Cmax <- c(Cmax, max(C, na.rm=TRUE))

Xr <- sweep(X,1,apply(X,1,mean),"-")
Cr <- abs(cor(Xr))
diag(Cr) <- NA
Crmax <- c(Crmax, max(Cr, na.rm=TRUE))
}
par(mfrow=c(1,1))
plot(Cmax, ylim=c(0,1), ylab="Cor. máxima", xlab="#Características",col=1,pch=1)
points(Crmax, ylim=c(0,1), col=2, pch=2)
legend("topright", legend=c("Original","Centro-fila"),pch=1:2,col=1:2)

EDICIÓN

Después de buscar en Google, llegué a esta página donde las simulaciones muestran un comportamiento similar y propone que la correlación introducida por el centrado en la media de las filas sea $-1/(p-1)$.

Answer 3

La normalización por filas tiene un nombre: escalado ipsativo, que normalmente implica reescalar un conjunto de características ya sea dividiéndolas por el valor máximo del conjunto o restando la media de las características. Hay muchas motivaciones para elegir este enfoque de transformación de datos, pero la principal de ellas es que condiciona las características en relación a las características únicas del individuo (la fila o unidad de análisis).

Answer 4

Existen varias formas de normalización de filas y el OP no está especificando cuál tiene en mente.

Una forma específica de normalización de filas (normalización de la norma euclidiana) donde cada fila se normaliza (dividida por su norma euclidiana) es bastante popular.

Las razones para usar esta forma de normalización de filas están bien resumidas en la sección $3.2$ de este artículo [0]:

Denotamos por $\pmb x$ un vector de fila centrado de $p$ variables y

$$r(\pmb x)=||\pmb x||^{-1}_2\pmb x\label{a}\tag{0}$$

el vector normalizado por fila. Considera qué es lo que esta transformación hace con tus datos geométricamente. Geométricamente, si tus datos originales tienen $p>1$ variables y están centrados, al aplicar la normalización de fila euclidiana, estás proyectando tus datos en la superficie del círculo unitario de $p$ dimensiones.

Por ejemplo, si tus datos originales están centrados (como los puntos negros en esta imagen) y aplicas normalización de filas, obtienes las estrellas rojas.

library(car)
p = 2
n = 1000
m = 10
C = matrix(.9, p, p)
diag(C) = 1
set.seed(123)
x = matrix(runif(n * p, -1, 1), n, p) %*% chol(C)
z = sweep(x, 1, sqrt(rowSums(x * x)), FUN = '/')
plot(rbind(x, z), pch = 16, type = 'n', ann = FALSE, xaxt = 'n', yaxt = 'n')
points(x, pch = 16)
points(z, pch = 8, col = 'red')

Los puntos verdes representan un pequeño número de valores atípicos en los datos originales. Si aplicas la transformación de normalización de filas sobre ellos, obtienes las estrellas azules.

x_1 = sweep(matrix(runif(m * p, -1, 1), m, p), 2, c(2, -2))
z_1 = sweep(x_1, 1, sqrt(rowSums(x_1 * x_1)), FUN = '/')
plot(rbind(x, x_1, z, z_1), pch = 16, type = 'n', ann = FALSE, xaxt = 'n', yaxt = 'n')
points(x, pch = 16)
points(x_1, pch = 16, col = 'green')
points(z, pch = 8, col = 'red')
points(z_1, pch = 8, col = 'blue')

Ahora las ventajas de esta transformación están claras. La proyección en el círculo unitario atenúa el efecto de los valores atípicos. Si tus datos originales $x$ provienen de un modelo centrado $\mathcal{F}$ exceptuando unos pocos valores atípicos lejanos (como los puntos verdes), entonces cualquier estimación de la forma de tus datos basada en $x$ será afectada por los valores atípicos.

Si basas tus estimaciones en los datos normalizados $z$ (las estrellas, rojas y azules), los valores atípicos (ahora mapeados como las estrellas azules) tienen menos influencia para afectar tus estimaciones.

Puedes ver esto de forma más clara comparando las matrices de forma (o elipses de contorno) ajustadas sucesivamente a los datos, su versión contaminada y la transformación normalizada de las mismas:

ellipse(crossprod(rbind(x, x_1)) / (n + m - 1) / det(crossprod(rbind(x, x_1)) / (n + m - 1))^(1 / p), center = rep(0, p), col = 'green', radius = 1)
ellipse(crossprod(rbind(z, z_1)) / (n + m - 1) / det(crossprod(rbind(z, z_1)) / (n + m - 1))^(1 / p), center = rep(0, p), col = 'red', radius = 1)
ellipse(crossprod(rbind(x)) / (n - 1) / det(crossprod(rbind(x)) / (n - 1))^(1 / p), center = rep(0, p), col = 'black', radius = 1)

Como puedes ver, la elipse ajustada a los datos transformados contaminados (elipse roja) es una mejor estimación de la matriz de forma de los datos no contaminados (elipse negra) que la obtenida a partir de los datos contaminados (elipse verde). Esto se debe a que las estrellas verdes tienen menos influencia sobre la elipse roja (construida a partir de los datos transformados $z$) que en la verde (construida a partir de los datos originales $x$).

• [0] S. Visuri, V. Koivunen, H. Oja (2000). Sign and rank covariance matrices, Journal of Statistical Planning and Inference Volume 91, Issue 2, 557–575.