Hay que recordar que el SI se define para facilitar su uso y la familiaridad humana. Los sistemas de unidades naturales tienen dos problemas en este sentido: es difícil seguir la pista de las unidades y, por tanto, evitar errores triviales como llamar a una longitud volumen o a un tiempo frecuencia, y las constantes implicadas son o bien impracticablemente enormes o bien impracticablemente diminutas a escala humana, lo que hace que las unidades también tengan un tamaño impracticable. Por eso el SI define las unidades que define.
La longitud y el tiempo se mantienen diferenciados porque el factor de conversión entre ambos (la velocidad de la luz) es ridículamente enorme. Un segundo-luz equivale a unos trescientos mil kilómetros, lo cual es demasiado. Y aunque un nanosegundo de luz equivale a unos treinta centímetros, un nanosegundo es demasiado pequeño. En consecuencia, damos a la velocidad de la luz una unidad (metros por segundo) y un valor numérico que nos permite alternar fácilmente entre los valores predefinidos de segundo y metro, de modo que podemos desechar esas definiciones y utilizar la nueva, basada en la velocidad de la luz.
Y si crees que la longitud y el tiempo lo tienen mal, recuerda que la masa y la energía tienen el mismo factor de conversión, pero al cuadrado . Un kilogramo cuadrado de luz equivale a unos noventa mil millones de millones de julios, una cantidad de energía que nunca alcanzaremos, salvo posiblemente en nuestras fantasías más salvajes. Y si intentamos ir a la inversa, nos encontramos con una unidad de masa aún más pequeña que un nanosegundo. Así que en lugar de utilizar la velocidad de la luz para convertir entre masa y energía, utilizamos la relación entre un metro y un segundo.
Por supuesto, la energía y el tiempo están relacionados por la constante de Planck, o el "cuanto de acción" (me acabo de inventar ese término), pero es ridículamente pequeña, incluso más de lo que la velocidad de la luz es ridículamente enorme. Así que hacemos lo mismo, le damos una unidad (julio-segundo) y un valor numérico que nos permite cambiar fácilmente entre los valores predefinidos de julio y segundo, para poder desechar esas definiciones y utilizar la nueva, basada en Planck.
Salvo que en realidad nos resulta mucho más fácil medir directamente la masa que la energía, así que medimos un kilogramo, lo multiplicamos por un metro por segundo al cuadrado (no confundir con metro por segundo al cuadrado) y llamamos que un julio, luego desechar el valor predefinido de un kilogramo para utilizar el nuevo, basado en Planck (lo que finalmente hicimos en 2019).
Luego están los amperios. La elección de definir una unidad eléctrica en lugar de simplemente derivarla de $LTM$ (longitud, tiempo, masa) era porque había múltiples formas de hacerlo, a diferencia, por ejemplo, de la energía, que siempre es $[M][L]^2[T]^{-2}$ . Claro, la definición gaussiana (electrostática) de carga era $[M]^{1/2}[L]^{3/2}[T]^{−1}$ pero el electro magnético definición de cargo era $[M]^{1/2}[L]^{1/2}$ .
La discrepancia se debe a qué relación consideras fundamental. ESU (unidades electrostáticas) parte de la ley de Coulomb; EMU (unidades electromagnéticas) parte de la ley de Ampere. Estos dos métodos crean unidades de carga que difieren en un factor de la velocidad de la luz, de ahí las diferentes unidades. El SI optó por la ley de Ampere porque era más fácil de medir, de ahí la elección del amperio en lugar del culombio, pero desde entonces ha decidido contar electrones por segundo, decidiendo que la unidad fundamental es el cuanto de carga. Por cierto, por eso no se habla de "unidades de carga de color" o "unidades de carga de sabor"; los recuentos de cuantos de carga se tratan como recuentos sin unidades, eludiendo toda la cuestión.
Del mismo modo, es posible que haya oído que "la temperatura es sólo energía". No lo es, es energía por unidad de entropía . Lo que ocurre es que la entropía es fundamentalmente una descripción de la información, por lo que puede reducirse a un recuento sin unidades de "bits" o "grados de libertad". Del mismo modo, la cantidad de sustancia es sólo contar partículas; el mol es simplemente un número conveniente para cambiar entre el reino de las partículas y el reino de las sustancias. de las sustancias. En cuanto a la intensidad luminosa, el propio concepto depende de la sensibilidad del ojo humano; las candelas no pasarían desapercibidas fuera de la fotometría, y de hecho no lo son.

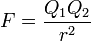
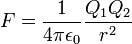



0 votos
¿Ha pensado en las Unidades Naturales? es.wikipedia.org/wiki/Unidades_naturales
0 votos
Sí, las unidades Planck son un ejemplo de unidades naturales. La cuestión es que no entiendo cómo las dimensiones de las cantidades pueden ser diferentes en distintos sistemas de unidades.
0 votos
Los dos sistemas que mencionas son diferentes porque las unidades gaussianas incorporan muchas de las constantes naturales en las unidades. La carga es en términos de masa, longitud y tiempo sólo porque la constante $\epsilon_0$ se le ha aplicado (esencialmente)
2 votos
Este documento podría ser muy interesante para usted arxiv.org/abs/physics/0110060
1 votos
Ese periódico es genial. He aquí una cita ilustrativa del mismo: "El SI puede ser útil desde el punto de vista de la tecnología y la metrología, pero desde el punto de vista de la física pura cuatro de sus siete unidades básicas son evidentemente derivadas. La corriente eléctrica es el número de electrones en movimiento por segundo. La temperatura depende de un factor de conversión".
0 votos
No todos los "sistemas" son iguales. ¿Imagina que el SI se hubiera definido antes del descubrimiento de la electricidad? En ese sistema no habría ni culombio ni amperio, lo que variaría el número de magnitudes fundamentales. Por ejemplo, el metro se define ahora en función de la velocidad de la luz, pero el metro era una "unidad fundamental" antes de que se conociera la velocidad de la luz (o incluso de que se supiera que era constante).