Diferencia entre modelos lineales generalizados y modelos lineales generalizados mixtos

Question

Estoy preguntándome cuáles son las diferencias entre GLMs mixtos y no mixtos. Por ejemplo, en SPSS el menú desplegable permite a los usuarios ajustar cualquiera de los siguientes:

• analizar-> modelos lineales generalizados-> modelos lineales generalizados &
• analizar-> modelos mixtos-> lineal generalizado

¿Tratan de manera diferente los valores faltantes?

Mi variable dependiente es binaria y tengo varias variables independientes categóricas y continuas.

Answer 1

El advenimiento de modelos lineales generalizados nos ha permitido construir modelos de regresión de datos cuando la distribución de la variable de respuesta no es normal, por ejemplo, cuando su variable dependiente es binaria. (Si desea saber un poco más sobre GLiMs, escribí una respuesta bastante extensa aquí, que puede ser útil aunque el contexto difiera). Sin embargo, un GLiM, por ejemplo, un modelo de regresión logística, asume que sus datos son independientes. Por ejemplo, imagine un estudio que analiza si un niño ha desarrollado asma. Cada niño contribuye con un punto de datos al estudio, ya sea que tenga asma o no. A veces los datos no son independientes, sin embargo. Considere otro estudio que analiza si un niño tiene un resfriado en varios momentos durante el año escolar. En este caso, cada niño contribuye con varios puntos de datos. En un momento dado, un niño puede tener un resfriado, luego no, y más tarde puede tener otro resfriado. Estos datos no son independientes porque provienen del mismo niño. Para analizar adecuadamente estos datos, debemos de alguna manera tener en cuenta esta no independencia. Hay dos formas: Una forma es utilizar las ecuaciones de estimación generalizadas (que no mencionas, así que pasaremos por alto). La otra forma es utilizar un modelo lineal mixto generalizado. Los GLiMMs pueden tener en cuenta la no independencia al agregar efectos aleatorios (como señala @MichaelChernick). Por lo tanto, la respuesta es que tu segunda opción es para datos de medidas repetidas no normales (o de otra manera no independientes). (Debo mencionar, en concordancia con el comentario de @Macro, que los modelos mixtos lineales general-izados incluyen modelos lineales como un caso especial y por lo tanto pueden usarse con datos normalmente distribuidos. Sin embargo, en el uso típico, el término connota datos no normales).

Actualización:(El OP también ha preguntado sobre GEE, así que escribiré un poco sobre cómo se relacionan entre sí.)

Aquí tienes una visión general básica:

• Un GLiM típico (usaré la regresión logística como caso prototípico) te permite modelar una respuesta binaria independiente como una función de los covariables
• Un GLMM te permite modelar una respuesta binaria no independiente (o agrupada) condicional a los atributos de cada grupo individual como una función de los covariables
• Las GEE te permiten modelar la respuesta media de la población de datos binarios no independientes como una función de los covariables

Dado que tienes múltiples pruebas por participante, tus datos no son independientes; como mencionas correctamente, "[l]as pruebas dentro de un participante son propensas a ser más similares en comparación con todo el grupo". Por lo tanto, debes usar un GLMM o las GEE.

Entonces, la cuestión es cómo elegir si GLMM o GEE sería más apropiado para tu situación. La respuesta a esta pregunta depende del tema de tu investigación, específicamente, el objetivo de las inferencias que esperas hacer. Como mencioné anteriormente, con un GLMM, los betas te están informando sobre el efecto de un cambio de una unidad en tus covariables en un participante particular, dado sus características individuales. Por otro lado, con las GEE, los betas te están informando sobre el efecto de un cambio de una unidad en tus covariables en el promedio de las respuestas de toda la población en cuestión. Esta es una distinción difícil de entender, especialmente porque no existe tal distinción con los modelos lineales (en cuyo caso son la misma cosa).

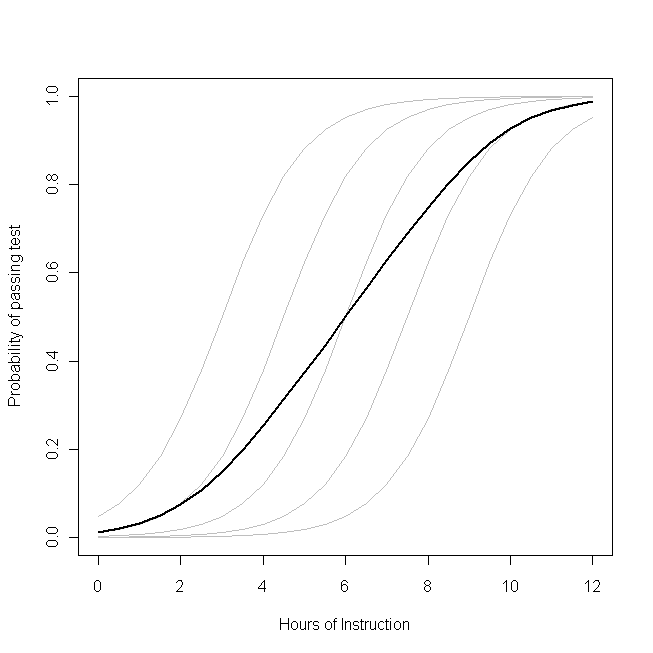
Una forma de tratar de entender esto es imaginar el promedio de tu población en ambos lados del signo igual en tu modelo. Por ejemplo, este podría ser un modelo: $$ \text{logit}(p_i)=\beta_{0}+\beta_{1}X_1+b_i $$ donde: $$ \text{logit}(p)=\ln\left(\frac{p}{1-p}\right),~\&~~b\sim\mathcal N(0,\sigma^2_b) $$ Hay un parámetro que rige la distribución de la respuesta ($p$, la probabilidad, con datos binarios) en el lado izquierdo para cada participante. En el lado derecho, hay coeficientes para el efecto de la covariable[s] y el nivel base cuando la covariable[s] es igual a 0. Lo primero que hay que notar es que el intercepto real para cualquier individuo específico no es $\beta_0$, sino $(\beta_0+b_i)$. Pero ¿qué importa? Si asumimos que los $b_i$'s (el efecto aleatorio) se distribuyen normalmente con una media de 0 (como hemos hecho), ciertamente podemos promediar sobre estos sin dificultad (sería simplemente $\beta_0$). Además, en este caso no tenemos un efecto aleatorio correspondiente para las pendientes y, por lo tanto, su promedio es simplemente $\beta_1$. Así que el promedio de los intercepciones más el promedio de las pendientes debe ser igual a la transformación logit del promedio de los $p_i$'s a la izquierda, ¿no? Desafortunadamente, no. El problema es que en medio de esos dos está el $\text{logit}$, que es una transformación no lineal. (Si la transformación fuera lineal, serían equivalentes, por eso este problema no ocurre para los modelos lineales). El siguiente gráfico aclara esto:
Imagina que este gráfico representa el proceso generador de datos subyacente para la probabilidad de que un pequeño grupo de estudiantes pueda aprobar un examen sobre un tema con una cierta cantidad de horas de instrucción en ese tema. Cada una de las curvas grises representa la probabilidad de aprobar el examen con diferentes cantidades de instrucción para uno de los estudiantes. La curva en negrita es el promedio de toda la clase. En este caso, el efecto de una hora adicional de enseñanza condicional a los atributos del estudiante es $\beta_1: el mismo para cada estudiante (es decir, no hay una pendiente aleatoria). Sin embargo, ten en cuenta que la habilidad base de los estudiantes difiere entre ellos, probablemente debido a diferencias en cosas como el coeficiente intelectual (es decir, hay una intercepción aleatoria). La probabilidad promedio para toda la clase, sin embargo, sigue un perfil diferente que los estudiantes. El resultado sorprendentemente contraintuitivo es este: una hora adicional de instrucción puede tener un efecto considerable en la probabilidad de que cada estudiante apruebe el examen, pero tener relativamente poco efecto en la proporción total probable de estudiantes que aprueban. Esto se debe a que algunos estudiantes pueden haber tenido ya una gran posibilidad de aprobar, mientras que otros aún podrían tener poca probabilidad.

La pregunta de si debes usar un GLMM o las GEE es la pregunta de qué función quieres estimar. Si quieres saber sobre la probabilidad de que un estudiante dado apruebe (si, por ejemplo, eres el estudiante, o el padre del estudiante), debes usar un GLMM. Por otro lado, si quieres saber sobre el efecto en la población (si, por ejemplo, eres el profesor, o el director), deberías usar las GEE.

Para obtener otra discusión más detallada matemáticamente sobre este material, consulta esta respuesta de @Macro.

Answer 2

La clave es la introducción de efectos aleatorios. El enlace de Gung lo menciona. Pero creo que debería haber sido mencionado directamente. Esa es la diferencia principal.

Answer 3

Te sugiero que también examines las respuestas a una pregunta que hice hace algún tiempo:

Modelo Lineal General vs. Modelo Lineal Generalizado (¿con una función de enlace de identidad?)