¿Es la distancia de Mahalanobis equivalente a la distancia euclidiana en los datos rotados por PCA?

Question

Me han llevado a creer (ver aquí y aquí) que la distancia de Mahalanobis es igual a la distancia euclidiana en los datos rotados por PCA. En otras palabras, tomando datos normales multivariados $X$, la distancia de Mahalanobis de todos los $x$ desde cualquier punto dado (digamos $\mathbf{0}$) debería ser la misma que la distancia euclidiana de las entradas de $X^{rot}$ desde $\mathbf{0}$, donde $X^{rot}$ es el producto de los datos y la matriz de rotación de PCA.

1. ¿Es esto cierto?

Mi código a continuación me está sugiriendo que no lo es. En particular, parece que la varianza de la distancia de Mahalanobis alrededor de la distancia PCA-Euclidiana está aumentando en la magnitud de la distancia PCA-Euclidiana. ¿Es esto un error de codificación, o una característica del universo? ¿Tiene algo que ver con la imprecisión en una estimación de algo? ¿Algo que se eleva al cuadrado?

N=1000
cr = runif(1, min=-1, max=1)
A = matrix(c(1,cr,cr,1),2)
e<-mvrnorm(n = N, rep(0,2), A)
mx = apply(e, 2, mean)
sx = apply(e, 2, sd)
e = t(apply(e, 1, function(X){(X-mx)/sx}))
plot(e[,1], e[,2])
dum<-rep(0,2)
md = mahalanobis(e, dum, cov(e))

pc = prcomp(e, center=F, scale=F)
d<-as.matrix(dist(rbind(dum, pc$x), method='euclidean', diag=F))
d<-d[1,2:ncol(d)]
plot(d, md^.5)
abline(0,1)

2. Si la respuesta a lo anterior es cierta, ¿se puede usar la distancia euclidiana PCA-rotada como un sustituto de la distancia de Mahalanobis cuando $p>n$?

Si no, ¿existe una métrica similar que capture la distancia multivariada, escalada por correlación, y para la cual existan resultados de distribución que permitan el cálculo de la probabilidad de una observación?

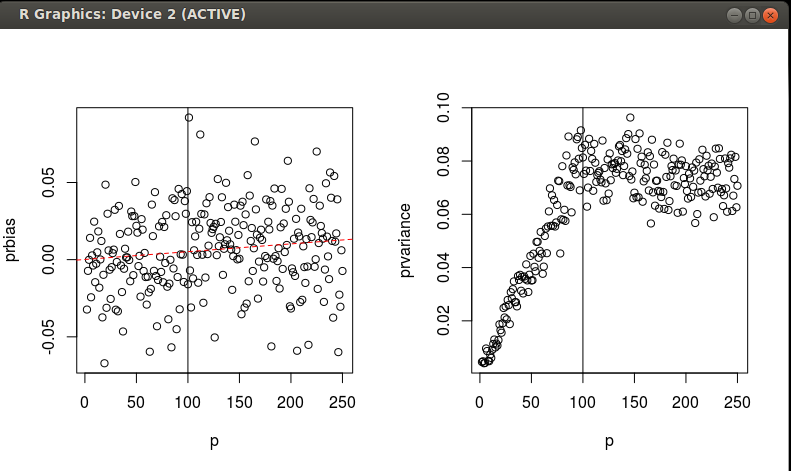
EDICIÓN He ejecutado algunas simulaciones para investigar la equivalencia de MD y SED en datos escalados/rotados a lo largo de un gradiente de n y p. Como mencioné anteriormente, estoy interesado en la probabilidad de una observación. Espero encontrar una buena forma de obtener la probabilidad de una observación que sea parte de una distribución normal multivariada, pero para la cual tengo datos $nligeramente sesgado de la MD, con una buena cantidad de varianza que parece dejar de aumentar cuando $p=N$.

f = function(N=1000,n,p){
  a = runif(p^2,-1,1)
  a = matrix(a,p)
  S = t(a)%*%a
  x = mvrnorm(N, rep(0,p), S)
  mx = apply(x, 2, mean)
  sx = apply(x, 2, sd)
  x = t(apply(x, 1, function(X){(X-mx)/sx}))
  Ss = solve(cov(x))
  x = x[sample(1:N, n, replace=F),]
  md = mahalanobis(x, rep(0, p), Ss, inverted=T)
  prMD<-pchisq(md, df = p) 
  pc = prcomp(x, center=F, scale=F)
  d<-mahalanobis(scale(pc$x), rep(0, ncol(pc$x)), diag(rep(1, ncol(pc$x))))
  prPCA<-pchisq(d, df = min(p, n))#N is the number of PCs where N

`

Dos preguntas: 1. ¿Algún comentario sobre lo que estoy encontrando en estas simulaciones? 2. ¿Alguien puede formalizar lo que estoy encontrando con una expresión analítica para el sesgo y la varianza en función de n y p? Aceptaría una respuesta que haga esto.

`

Answer 1

La distancia de Mahalanobis es equivalente a la distancia euclidiana en los datos transformados por el PCA (¡no solo rotados por el PCA!), donde por "transformados por el PCA" me refiero a (i) primero rotados para volverse no correlacionados, y (ii) luego escalados para estandarizarse. Esto es lo que @ttnphns dijo en los comentarios anteriores y lo que tanto @DmitryLaptev como @whuber quisieron decir y explicitamente escribieron en sus respuestas que enlazaste (uno y dos), así que te animo a releer sus respuestas y asegurarte de que este punto quede claro.

Esto significa que puedes hacer que tu código funcione simplemente reemplazando pc$x con scale(pc$x) en la cuarta línea desde abajo.

Respecto a tu segunda pregunta, con $n

Lo que se puede hacer es enfocarse exclusivamente en el subespacio donde realmente se encuentran los datos, y definir la distancia de Mahalanobis en este subespacio. Esto es equivalente a hacer PCA y mantener solo los componentes no nulos, que es lo que creo que sugeriste en tu pregunta #2. Así que la respuesta a esto es sí. Sin embargo, no estoy seguro de cuán útil pueda ser esto en la práctica, ya que es probable que esta distancia sea muy inestable (los autovalores cercanos a cero se conocen con muy mala precisión, pero van a ser invertidos en la fórmula de Mahalanobis, pudiendo producir errores graves).

Answer 2

La distancia de Mahalanobis es la distancia Euclidiana escalada cuando la matriz de covarianza es diagonal. En PCA, la matriz de covarianza entre componentes es diagonal. La distancia Euclidiana escalada es la distancia Euclidiana donde las variables fueron escaladas por sus desviaciones estándar. Ver p.303 en Enciclopedia de Distancias, un libro muy útil, por cierto.

Parece que estás intentando usar la distancia Euclidiana en el subconjunto de factores de PCA. Probablemente redujiste la dimensionalidad usando PCA. Puedes hacerlo, pero habrá un cierto error introducido que es "proporcional" a la proporción de la varianza que es explicada por tus componentes de PCA. También tendrás que ajustar la distancia por la escala (es decir, las varianzas explicadas), por supuesto.