Ayuda con el análisis de datos de conjuntos de datos pequeños

Question

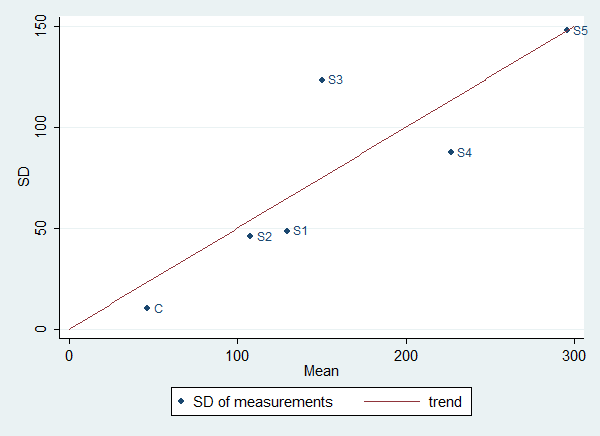
Tengo el siguiente conjunto de datos (valores triplicados de 5 mediciones independientes y valores duplicados de un control):

Muestra 1    Muestra 2   Muestra 3    Muestra 4    Muestra 5    C
181.8       58.2       288.9       273.2       290.9      53.9
120.3       116.8      108.9       281.3       446        39.6
86.1        148.5      52.9        126         150.3

Las seis condiciones son la producción independiente de un producto químico en seis microorganismos diferentes.

Mi objetivo era determinar si la producción del químico es significativamente mayor en las Muestras 1 - 5 que en C (control).

Al principio, realicé la media, la desviación estándar y la prueba t (una cola). Aunque las barras de error de la desviación estándar son grandes, dos de las muestras tienen valores medios que son significativamente más altos que el de C.

Decidí realizar la mediana y la prueba de Wilcoxon-Mann-Whitney debido a mi preocupación por el tamaño de mis datos y las altas variaciones en las réplicas. Sin embargo, me sorprendió que la mediana y las pruebas de Wilcoxon-Mann-Whitney no revelaron resultados estadísticamente significativos.

Estaré feliz si alguien pudiera aconsejarme sobre la mejor manera de analizar este pequeño conjunto de datos.

Answer 1

Este es un conjunto de datos interesante. Parece ser una buena idea seguir el consejo de @whuber y realizar el análisis en la escala logarítmica. Sin embargo, hay más de una hipótesis aquí. De hecho, podrías tener la hipótesis

$$H_{0}:\text{las muestras 1-5 tienen la misma media y varianza en la escala logarítmica,}$$ $$\text{y esto es diferente de la media de control}$$

Pero también podrías tener:

$$H_{1}:\text{las muestras 1-3 tienen la misma media y varianza en la escala logarítmica,}$$ $$\text{y esto es diferente de la media de control, y las muestras 4-5 tienen}$$ $$\text{la misma media y varianza pero diferentes tanto del grupo de control}$$ $$\text{como de las muestras 1-3}$$

$H_{1}$ parece ser la hipótesis más plausible para mí según mi juicio. También podrías tener:

$$H_{2}:\text{las muestras 1-5 tienen medias y varianzas diferentes en la escala logarítmica}$$ $$\text{y son diferentes del grupo de control}$$

Cada una de estas hipótesis, si son verdaderas, constituiría algún tipo de resultado "significativo". En cualquier caso, una vez que hayas decidido que son diferentes, el interés entonces se desplaza a decir "bueno, ¿exactamente en qué son diferentes?".

Creo que tienes un resultado menos significativo porque estás probando $H_{2}$ que tiene muchos parámetros.

Para $H_0$ tenemos $\text{media}\pm\text{desviación estándar}$ de $5.0\pm 0.62$ y $3.8\pm0.22$, mostrando una clara diferencia, la estadística de Fisher de Behrens es $$T=\frac{5.0-3.8}{\sqrt{\frac{0.62^2}{15}+\frac{0.22^2}{2}}}=5.39$$

La estadística T de dos muestras es de aproximadamente $2.64$, pero la suposición de varianza igual no es respaldada por los datos, especialmente porque el grupo de control tenía con diferencia la menor varianza, y es casi el triple de la varianza de la muestra combinada.

Más adelante ya que tengo que parar por ahora...

Answer 2

Se podría utilizar una versión no paramétrica de ANOVA: esto se llama la prueba de Kruskal-Wallis. Se basa en clasificar todos los 17 resultados y calcular las clasificaciones medias dentro de cada grupo. La clasificación media de 2.0 entre los controles es obviamente más pequeña que cualquier otra clasificación media (que van desde 7 a 12). Sin embargo, el valor p de la prueba es solo 0.0937 (basado en una aproximación chi-cuadrado).

Dentro de cada grupo (incluido el control), las desviaciones estándar son aproximadamente la mitad de las medias (la "tendencia" en la figura).

Esto sugiere (y justifica) basar el análisis en los logaritmos de las concentraciones, para los cuales las desviaciones estándar del grupo serán aproximadamente estables. Esto proporciona 11 grados de libertad para estimar la variación, por lo que tener solo dos o tres mediciones por grupo no es una limitación. Esta observación (que usar logaritmos puede estabilizar los residuos) es importante por sí sola, porque indica la mejor manera de hacer estimaciones, cómo llevar a cabo futuros análisis sobre continuaciones de este experimento, y respalda la percepción de que la desviación estándar de las mediciones de control realmente es relativamente pequeña. (Eso de otra manera es una conclusión débil porque solo hay dos mediciones de control).

Regresión (o equivalente, ANOVA) de los registros contra los identificadores del grupo tiene un valor p general de 0.0521 (utilizando una prueba F con 5 y 11 grados de libertad). Esto es sugestivo pero no lo suficientemente bajo como para ser considerado "significativo" por la mayoría de las revistas. Sin embargo, esta es una prueba de dos lados, mientras que su hipótesis es unidireccional. Un ajuste burdo es reducir a la mitad el valor p para reflejar esto y reportar el resultado como "significativo" con p aproximadamente igual a 0.026.

Debido a que este ajuste burdo es simplemente una aproximación, podría reforzar la idea con una prueba de permutación. Volviendo a la idea de un análisis no paramétrico, preguntamos por la posibilidad de que la clasificación media de la medición de control sea 2.0 o menos bajo la hipótesis nula de que todos los 17 resultados estuvieran asociados aleatoriamente con las 17 mediciones. Esto es equivalente a que el control tenga las concentraciones más pequeñas primera y segunda o primera y tercera de las 17. La posibilidad del primer evento es $\binom{2}{2}/\binom{17}{2} = 1/136$ y la posibilidad del segundo evento es la misma, para un total de $2/136$, o 1.47%. Incluso podrías caracterizar conservadoramente los resultados como "todas las concentraciones de control estuvieron entre las tres más bajas". La posibilidad de esto es $\binom{3}{2} / \binom{17}{2}$, igual a 2.2%. En cualquier caso, tienes un resultado significativo para $p \lt 0.022$.

Answer 3

Hay un momento para hacer inferencias estadísticas formales de muestra a población, y un momento para simplemente informar sobre sus resultados descriptivos y permitir que su audiencia haga inferencias informales, o no, como lo consideren adecuado. Esto parece ser lo último. Con dos valores de control, estás a un paso de no tener variación en la que basar ningún hallazgo.

"Sin embargo, me sorprendió que las pruebas de mediana y Wilcoxon-Mann-Whitney no revelaran resultados estadísticamente significativos." Te recomiendo que te familiarices con la literatura sobre poder estadístico.