Por supuesto depende de la distancia y la cantidad de radiación, así que vamos a decir su alrededor 10.000 Rad. ¿Ahora, puede pared de ladrillo proteger a alguien detrás de él de tal radiación?
Respuestas
¿Demasiados anuncios?
barry
Puntos
131
Me centraré en los rayos gamma (y de alta energía de rayos X), ya que el alfa y beta partículas son fácilmente detenido. Los neutrones son un poco más complicados, ya que tienden a la atención acerca de que los núcleos de los que se están encontrando.
Teoría General
La respuesta es cualquier material puede bloquear los rayos gamma de tanto tiempo no es suficiente. De hecho, la cantidad de material es, básicamente, el único criterio que hay.
La cosa es que, cada vez que un rayo gamma fotón interactúa con un núcleo o un electrón, o sea es completamente perdido o se pierde algo de energía. Y los rayos gamma interactúa con nada a lo largo de su camino. No importa qué tipo de material están en - ya que sus longitudes de onda son tan cortos, que no "ven" el molecular y estructura a gran escala. La fracción de rayos gamma de energía que pasa a través de algún asunto, entonces, sólo se preocupa por la columna de la densidad de la materia. Hay un aumento exponencial de la dependencia - si la pared es dejar la mitad de la radiación a través de, duplicando su espesor será el resultado en sólo un trimestre.
Por ejemplo, si usted tenía una pared de ladrillos que era lo suficientemente gruesa que un $1\ \mathrm{cm}^2$ core a través de ella había una masa de $1\ \mathrm{kg}$ (aproximadamente el $4\ \mathrm{m}$ gruesa, para algunas de las "típicas" de ladrillo), entonces sería el equivalente, en términos de rayos gamma potencia de frenado, para
- Un $1\ \mathrm{m}$ espesor de pared de plomo,
- Un $10\ \mathrm{m}$ espesor de pared de agua, o
- La atmósfera (es decir, la misma atenuación, como entre un punto al nivel del mar y un punto en la órbita directamente por encima de uno).
Cuánto los asuntos materiales
Mi reclamo de independencia de material es, huelga decirlo, un poco de una simplificación. Tal vez el mayor de supervisión es la variación de los electrones a la relación entre la masa (lo que es equivalente, $Z/A$ de los átomos involucrados). En la medida en que esta relación es constante (y es buena es para todo, desde helio a cerca de níquel), el número de partículas que puede detener los rayos gamma es proporcional a la masa de la columna de densidad, suponiendo que las interacciones están dominados por la dispersión de Compton. Si la energía de los rayos gamma es en la producción de par régimen, esto podría depender más en el número de núcleos en lugar de por número de electrones.
Vamos a poner estas declaraciones en forma gráfica. La figura de abajo, de Wikimedia, muestra cuánto fotones de alta energía son atenuadas (línea negra) al pasar a través de el hierro, en función de cómo energético de los fotones. Las líneas de color indica las diferentes cosas que pueden suceder a la de los fotones, y se suman a la línea negra.
Ahora echemos un vistazo a algo más cercano a ladrillo. El US Instituto Nacional de Estándares y Tecnología (NIST) ha recopilado una gran cantidad de datos sobre este tipo de cosas aquí[1]. Mientras que yo no podía encontrar los datos de ladrillo"," ellos tienen para concreto aquí, que se reproducen a continuación.
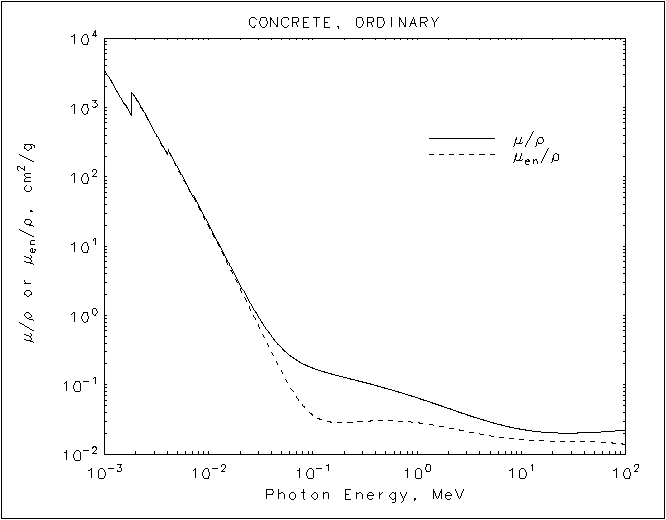
Estamos interesados en la línea sólida, que muestra la pérdida de energía por la radiación. La línea discontinua muestra la energía tomada por el material, que puede ser un poco menos si la energía se pierde, dicen, para escapar de los neutrinos. (La línea discontinua es más importante en materiales biológicos, donde la atención la cantidad de energía que se deposita más de cuánto se pierde por la explosión.) Tenga en cuenta que es básicamente el mismo que para el hierro. De hecho, para demostrar que estos números no cambian mucho, como afirmó anteriormente, a continuación se presentan las cifras para el agua (se encuentra aquí) y el aire (se encuentra aquí).
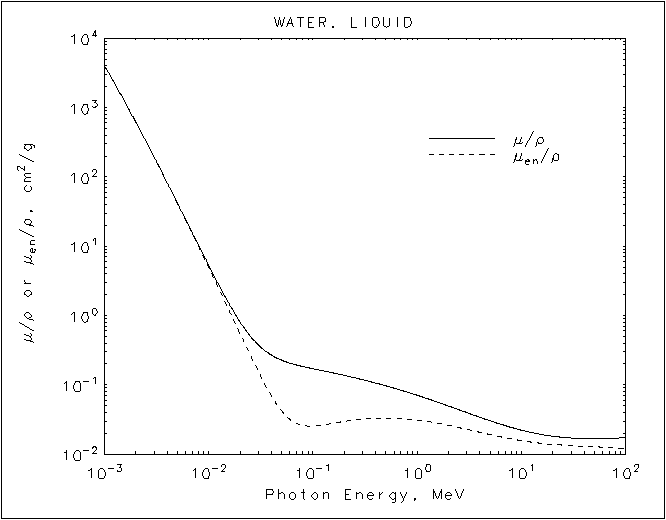
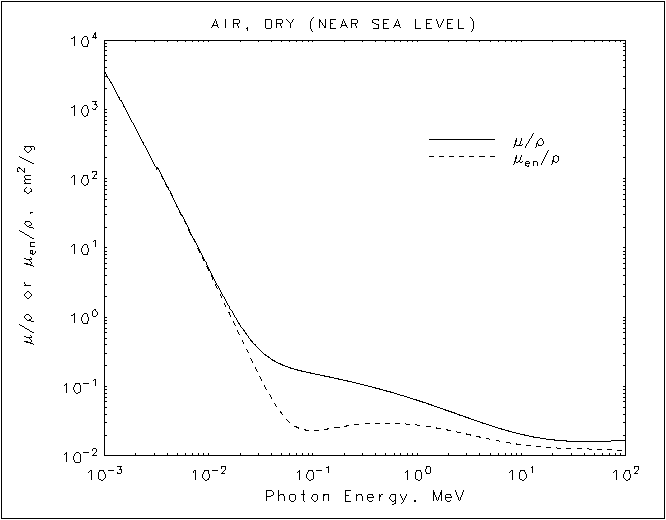
Conectar los números
Entonces, ¿cómo son exactamente estos diagramas utilizados? Vamos a tomar el hormigón gráfico, y vamos a tomar la densidad de ladrillo a ser $\rho = 2\ \mathrm{g}/\mathrm{cm}^3$. Multiplicando las ordenadas en la tabla por esta densidad se da el coeficiente de atenuación. Supongamos que estamos tratando con fotones de energía $10^{-2}\ \mathrm{MeV} = 10\ \mathrm{keV}$. A continuación, el coeficiente de atenuación es $$ \mu_{10\ \mathrm{keV}} = (10^2\ \mathrm{cm^2}/\mathrm{g}) (2\ \mathrm{g}/\mathrm{cm}^3) = 2\times10^2\ \mathrm{cm}^{-1}. $$ Si, por el contrario, estamos tratando con la mayor energía de los fotones, en torno a $10\ \mathrm{MeV}$ o más, entonces el coeficiente de atenuación es $$ \mu_{10\ \mathrm{MeV}} = (2\times10^{-2}\ \mathrm{cm^2}/\mathrm{g}) (2\ \mathrm{g}/\mathrm{cm}^3) = 4\times10^{-2}\ \mathrm{cm}^{-1}. $$ Para estar en el lado seguro, vamos a utilizar el último valor, que corresponde a la de más difícil dejar de fotones, ya que no puedo encontrar ningún dato sobre el espectro de la radiación ionizante.
Ahora una pared con espesor de $x$ permitirá una fracción $\mathrm{e}^{-\mu x}$ de la radiación a través de. Con $\mu = 4\times10^{-2}\ \mathrm{cm}^{-1}$$x = 15\ \mathrm{cm}$, esto viene a ser $55\%$. Es decir, que la pared no incluso dejar la mitad de la gamma de alta energía de la radiación. (Si utiliza el otro vale de $\mu$, usted va a encontrar una respuesta tan cerca de $0$ que la mayoría de las calculadoras no pueden distinguir los dos; de baja energía de la radiación es completamente detenido por este muro.)
Breve digresión sobre las unidades de
Hay cuatro etapas de cálculo de los efectos de la radiación, como se explica muy bien por la Comisión Reguladora Nuclear (NRC) en esta página. Cada uno tiene una unidad del SI y el otro utiliza comúnmente unidad de medida, que es la razón por la medición de la radiación puede ser tan confuso. Una fuente de radiación tiene su radiactividad medida en bequerelios ($\mathrm{Bq}$) o curios ($\mathrm{Ci}$). La cantidad de radiación que viaja lejos de la fuente se mide en coulombs por kilogramo ($\mathrm{C}/\mathrm{kg}$) o r ($\mathrm{R}$). La cantidad de energía absorbida por el cuerpo (parece que los de las líneas de puntos en las cifras anteriores) se mide en grays ($\mathrm{Gy}$) o rads ($\mathrm{rad}$). Finalmente, el último par puede ser ponderado por algún factor para dar cuenta de los diferentes tipos de radiación que es más perjudicial debido a que inducen las reacciones secundarias en su cuerpo. El resultado es sieverts ($\mathrm{Sv}$) y rems ($\mathrm{rem}$). Afortunadamente, que el peso es generalmente llevado a ser $1$ de los rayos gamma. Citando el NRC,
"Para fines prácticos, $1\ \mathrm{R}$ (exposición) = $1\ \mathrm{rad}$ (dosis absorbida) = $1\ \mathrm{rem}$ o $1000\ \mathrm{mrem}$ (dosis equivalente)."
Poner todo junto
El $15\ \mathrm{cm}$ pared de reducir la cantidad de radiación que llega por $45\%$ en el peor de los casos (todos radiación de alta energía), lo que significa que la energía absorbida por su cuerpo también será reducido por $45\%$, así como la dosis equivalente. Por lo tanto, usted recibiría aproximadamente $5500\ \mathrm{rem} = 55\ \mathrm{Sv}$. La rem artículo nos dice,
"Dosis superiores a $100\ \mathrm{rem}$ recibió más de un corto período de tiempo pueden causar síndrome de radiación aguda (ARS), posiblemente llevando a la muerte en cuestión de semanas."
Para reducir esto a la típica de la cantidad recibida en una tomografía computarizada, acerca de $1\ \mathrm{rem}$ según la NRC, se necesitaría un total espesor de la pared de $$ x = -\frac{1}{\mu} \log\left(\frac{1\ \mathrm{rad}}{10^4\ \mathrm{rad}}\right) \approx 230\ \mathrm{cm}. $$
[1] J. H. Hubbell y S. M. Seltzer. Tablas de Rayos X de la Masa Coeficientes de Atenuación de Masa y Energía-Coeficientes de Absorción de $1\ \mathrm{keV}$ $20\ \mathrm{MeV}$para los Elementos $Z = 1$ $92$ $48$Adicional de Sustancias de Interés Dosimétrico.
aceinthehole
Puntos
1460
Chris se dirigió a la materia básica de gammas, pero los neutrones son un caso especial, y uno de algún interés con las armas termonucleares. Debido a que no interactúan fuertemente con la carga eléctrica, los neutrones se dispersan y pierden energía, casi en su totalidad por contacto con la dispersión de los núcleos.
Que salir del barrio de la explosión con una considerable cantidad de energía cinética. Y lo pierde en una serie de (en su mayoría elástica) la interacción con los núcleos de el aire, la tierra y toda la infraestructura que permanece. Donde ellos interactúan inelastically suelen generar uno de los más energéticos que los rayos gamma.
Con sus diez minutos de período de semidesintegración son capaces de cubrir un montón de tierra, incluso después de que thermalize (pierden su energía cinética inicial, y entrar en equilibrio térmico con el material circundante) en parte debido a que viajar junto con cualquier masiva de los movimientos de masas de aire.
Eventualmente cualquiera de las caries ( $n \to p + e^- + \bar\nu$ ), que es relativamente pequeña de radiación beta o de captura (en su mayoría de hidrógeno--2.2 MeV de gamma-o de carbono--4.95 MeV).
Ahora aquí está la parte desagradable: tanto la inicial de energía de alta penetración y todo lo que el movimiento Browniano como el thermalized neutrones rebote en equilibrio es en gran parte sin blindaje, los neutrones pueden conseguir en casi cualquier lugar. Así que aquellos de captura de gammas puede ser generado en el interior de su protección o incluso dentro de su cuerpo. Ouch.
Para protegerse de neutrones que usted desea tantos núcleos como sea posible. La cera, el agua y los plásticos son opciones comunes. Para proteger contra los neutrones térmicos algunos denso material dopado con fuerte absorción de neutrones del agente. Borato los plásticos son buenos para los dos y son comunes en el reactor de blindaje. Especialmente con borato de PVC como el cloro es casi tan útil como el boro. Dada la reciente caída en el costo de gadolinio espero ver un creciente número de usos de la misma en el blindaje de neutrones de la aplicación.
