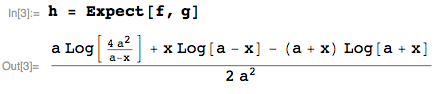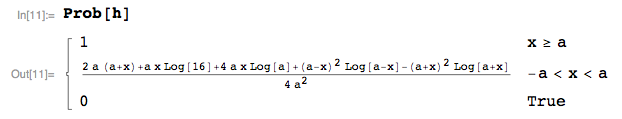¿Cuáles son la función de densidad de probabilidad y función de distribución acumulativa de un compuesto triangular de distribución con uniformemente distribuida modo, ambos apoyados en $(-a, a)$? I. e.,
$$ m \sim \mathrm{Unif}(-a, a) \\ X \sim \mathrm{Triang}(-a, a, m) $$
¿Tiene un nombre?
No es un Wigner semicírculo de distribución y está cerca de una escala, cambió distribución beta con $\alpha = \beta \approx 1.75$, pero estoy interesado en saber si se tiene una simple forma cerrada.
Dado: $X \sim \text{Triangular}(-a,m,a)$ con pdf $f(x)$:
donde el parámetro $m$, en vez de ser fijo, es en sí misma una variable aleatoria. En particular, $M \sim \text{Uniform}(-a,a)$, con pdf $g(m)$:
Luego, buscamos el parámetro de mezcla distribución $E_{g }\big[\;f (x \; \big | \;M =m )\big]$, lo que ha pdf decir $h(x)$:
donde yo estoy usando el Expect función de la mathStatica paquete de Mathematica para automatizar el cálculo. El dominio de apoyo es, por supuesto, $(-a,a)$.
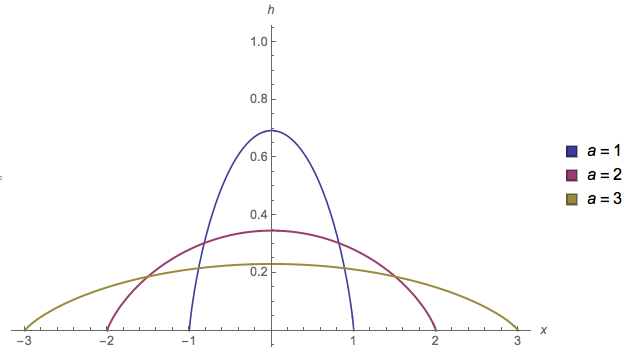
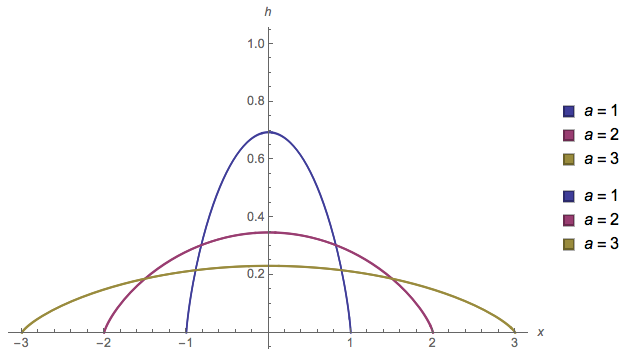
Para ilustrar, aquí es una parcela de la pdf $h(x)$, como parámetro de $a$ varía:
La cdf $P_h(X<x)$ es:
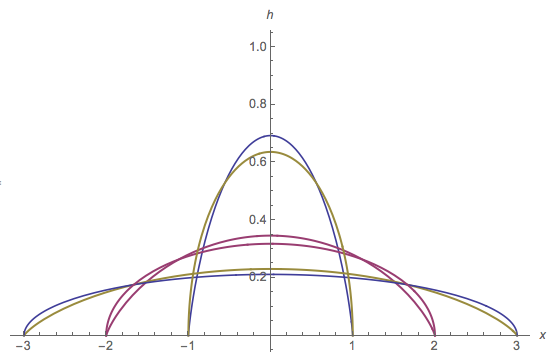
Comparación de semi-círculo de distribución
En el diagrama siguiente se compara el pdf de la solución exacta $h(x)$ a del semicírculo pdf que el OP se refiere. El pdf $h(x)$ es algo más picuda que la semi-círculo:
Comparación de ALIMENTACIÓN semi-círculo de distribución
Mientras que la forma funcional es diferente, se puede aproximar el pdf $h(x)$ muy bien con un poder semi-círculo de la distribución de la forma:
$$ \phi(x) = k \left(a^2-x^2\right)^{3/4}$$
where $k = \frac{\Gamma \left(\frac{9}{4}\right)}{\left(\sqrt{\pi }^{5/2}\right) \Gamma \left(\frac{7}{4}\right)}$
El ajuste es tan bueno que uno apenas puede ver ninguna diferencia perceptible:
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
