Es una pregunta sobre el comportamiento del portador libre en hojuelas de grafeno. (o puede ser llamado confinamiento de carga)
Supongamos que tenemos una hojuela de grafeno independiente perfecta con bordes en zigzag. Dado que hay dos subátomos (llamémoslos A, B) en cada celda unitaria. Los bordes terminarán, digamos, ABABAB (como se muestra en la figura).
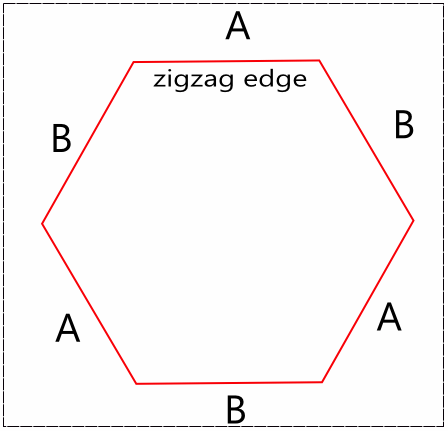
Mi pregunta es cómo calcular (entender) la función de onda electrónica en este sistema (solo considerando el caso de energía relativamente baja, el portador de carga se puede ver como fermiones sin masa). Otra forma de preguntar es qué tipo de condición de borde se debe usar para esos dos tipos de bordes. Según este artículo (pdf), el espalcamiento en el borde en zigzag no acopla los dos valles. Creo que solo podemos considerar una imagen de un valle (¿es esto cierto?), lo que significa que la ecuación de Dirac más simple $-i\hbar \nu_F\nabla \Psi_i=E\Psi_i$, donde $i=A,B$ (o ecuación de Klein-Gordon). Para simplificar, el efecto de spin aquí también se puede ignorar (sin campo magnético). No solo estoy preguntando sobre los estados de borde, también sobre los estados de energía más alta. Lo que me confunde es cómo distinguir esto del caso de partícula en una caja (partícula relativista, aquí me refiero).
Intuitivamente, creo que el electrón se comportará como una bola de billar dentro de la hojuela. Pero podría haber dos casos, ya sea que los electrones reboten entre los bordes A, B, o lo hagan solo en un tipo de borde, como rebotar solo en los bordes terminados con el subátomo A. ¿Se puede entender de esta manera? Si es así, ¿cuál de las dos imágenes es la real?
Espero que sea claro. Gracias.


