Esto me ha estado molestando por un tiempo...
Obviamente, para calcular el volumen/espacio ocupado por un mol de gas (ideal), tendrás que especificar la temperatura ($T$) y la presión ($P$), encontrar el valor de la constante de gas ($R$) con las unidades correctas e introducirlos en la ecuación del gas ideal $$PV = nRT.$$
¿El problema? Parece ser una especie de "sabiduría" común en todo Internet que un mol de gas ocupa $22.4$ litros de espacio. Pero las condiciones estándar (STP, NTP, o SATP) mencionadas carecen de consistencia en múltiples sitios/libros. Afirmaciones comunes: Un mol de gas ocupa,
- $\pu{22.4 L}$ en STP
- $\pu{22.4 L}$ en NTP
- $\pu{22.4 L}$ en SATP
- $\pu{22.4 L}$ tanto en STP como en NTP
Incluso Chem.SE está lleno de la "falsa creencia" de que un mol de gas ideal ocupa $\pu{22.4 L}$, o alguna extensión de ello.
Estando tan frustrado con esta situación, decidí calcular los volúmenes ocupados por un mol de gas ideal (basado en la ecuación del gas ideal) para cada una de las tres condiciones estándar; es decir: Temperatura y Presión Estándar (STP), Temperatura y Presión Normales (NTP) y Temperatura y Presión Ambiente Estándar (SATP).
Sabiendo que,
- STP: $\pu{0 ^\circ C}$ y $\pu{1 bar}$
- NTP: $\pu{20 ^\circ C}$ y $\pu{1 atm}$
- SATP: $\pu{25 ^\circ C}$ y $\pu{1 bar}$
Y usando la ecuación, $$V = \frac {nRT}{P},$$ donde $n = \pu{1 mol}$, por defecto (ya que estamos hablando de un mol de gas).
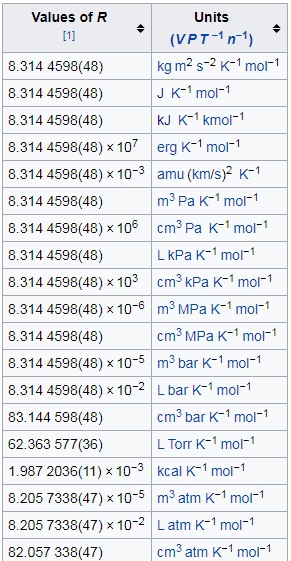
Tomaré los valores apropiados de la constante de gas $R$ de esta tabla de Wikipedia:
El volumen ocupado por un mol de gas debería ser:
-
En STP \begin{align} T &= \pu{273.0 K},& P &= \pu{1 bar},& R &= \pu{8.3144598 \times 10^-2 L bar K^-1 mol^-1}. \end{align> Introduciendo todos los valores, obtuve $$V = \pu{22.698475 L},$$ que para una aproximación razonable, da $$V = \pu{22.7 L}.
-
En NTP \begin{align> T &= \pu{293.0 K},& P &= \pu{1 atm},& R &= \pu{8.2057338 \times 10^-2 L atm K^-1 mol^-1}. \end{align> Introduciendo todos los valores, obtuve $$V = \pu{24.04280003 L},$$ que para una aproximación razonable, da $$V = \pu{24 L}.
-
En SATP \begin{align> T &= \pu{298.0 K},& P &= \pu{1 bar},& R &= \pu{8.3144598 \times 10^-2 L bar K^-1 mol^-1}. Introduciendo todos los valores, obtuve $$V = \pu{24.7770902 L},$$ que para una aproximación razonable, da $$V = \pu{24.8 L}.
En ninguno de los tres casos que analicé aparece la cifra mágica de "$\pu{22.4 L}." Dado que he visto tantas veces el dicho de "un mol ocupa $\pu{22.4 L}$ en STP/NTP," me pregunto si me he perdido de algo.
Mis preguntas:
- ¿Cometí errores en mis cálculos?
- (Si no cometí errores) ¿Por qué es tan extendida la idea de que un mol ocupa $\pu{22.4 L}$, a pesar de no aproximarse (suficientemente) a los valores que obtuve?



1 votos
Ver es.wikipedia.org/wiki/…
10 votos
Solo para mencionarlo, STP's a $T=273.15\mathrm{K}$ en lugar de $T=273.0\mathrm{K}$. Entiendo completamente que las personas a menudo truncan el $.15$ por brevedad, solo se ve un poco fuera de lugar junto a $R$ dado con 8 cifras significativas.