¿Por qué aparecen curvas de campana en todas partes?

Question

¿Por qué la mayoría de los gráficos de probabilidad muestran una curva de campana? Me he estado preguntando por qué... ¿Es algo natural, como la secuencia de Fibonacci?

Answer 1

¿Por qué la mayoría de los gráficos de probabilidad muestran una curva de campana?

Como sospecha, existe una tendencia natural a que las distribuciones tengan forma de campana.

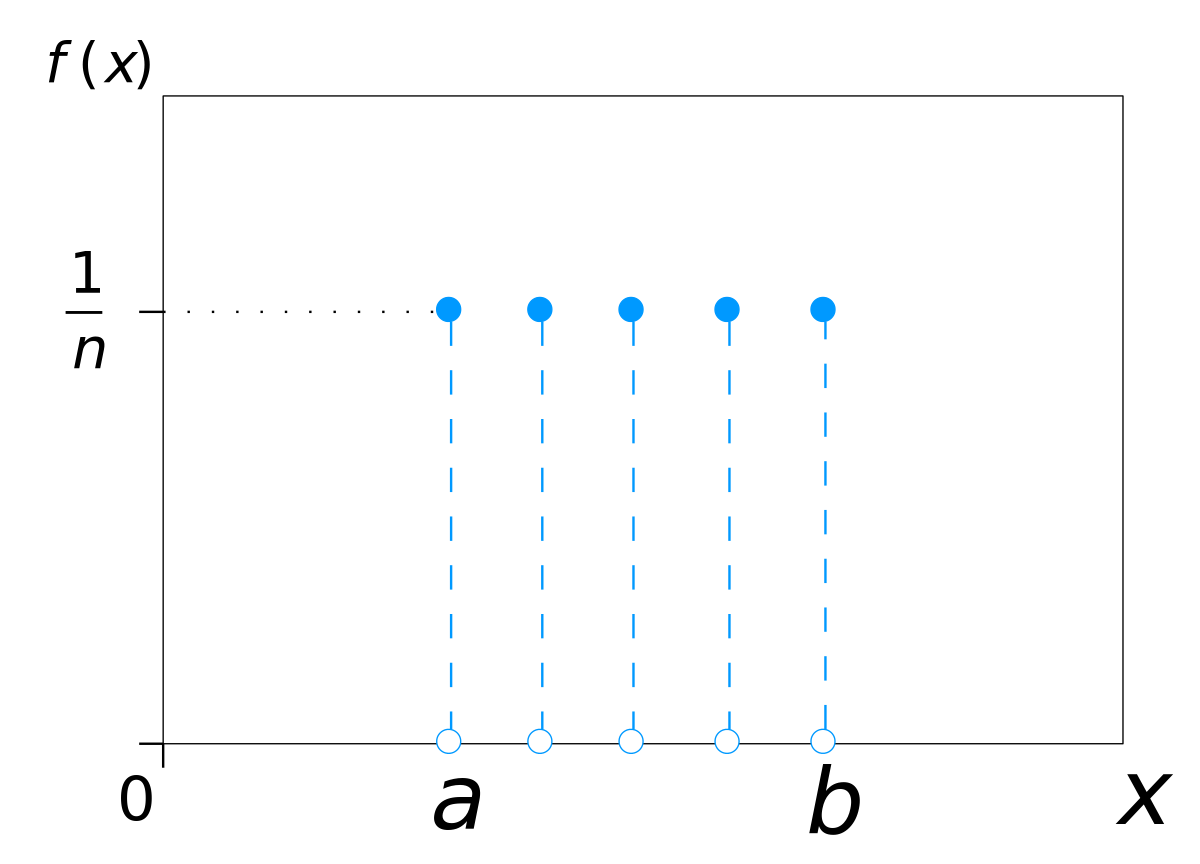
Algunas distribuciones no tienen forma de campana. Por ejemplo, el resultado de una tirada de un dado justo es un distribución uniforme discreta :

Por IkamusumeFan - Obra propia Este dibujo fue creado con LibreOffice Draw, CC BY-SA 3.0 , Enlace

La tirada de un dado es un proceso bastante sencillo. ¿Y la suma de dos dados? El Mago de las Probabilidades ilustra :

Empieza a parecerse un poco a una campana, ¿verdad? ¿Qué pasa con los totales de tres, o cuatro dados? Wolfram MathWorld ofrece una bonita ilustración :

Ya ves a dónde nos lleva esto. La naturaleza está llena de procesos complejos. ¿Cuánto mides? Depende de la genética, la nutrición, el ejercicio, las lesiones, la pérdida de masa ósea y muchas cosas más. En teorema central del límite espectáculos (véase Comentario de symplectomorphic más abajo) que al sumar la suma de un gran número de cosas, la distribución resultante no es una curva cualquiera con aspecto de campana, sino específicamente la distribución normal . O para cosas con combinación multiplicativa, el distribución logarítmica normal .

¿Por qué ocurre esto? Respuesta de mathreadler pistas que tiene que ver con convolvente distribuciones. La función de densidad de probabilidad de un solo dado es una función rectangular (técnicamente discreta, pero hagamos como si fuera continua). La suma de dos tiradas es entonces la convolución de dos funciones rectangulares.

Por Convolución_de_señal_de_caja_con_ella.gif : Brian Amberg obra derivada: Tinos ( hable ) - Convolución_de_señal_de_caja_con_ella.gif , CC BY-SA 3.0 , Enlace

Observa cómo el resultado (el triángulo negro) se parece al caso de dos dados anterior. Si a continuación conviertes este triángulo con otro rectángulo, obtienes tres dados. Cuantas más veces hagas esto, más se acercará el resultado a una distribución normal.

La función de densidad de probabilidad de la distribución normal es una función gaussiana, que tiene algunas propiedades elegantes:

• Una gaussiana convolucionada con una gaussiana es otra gaussiana.
• El producto de dos gaussianas es una gaussiana.
• La transformada de Fourier de una gaussiana es una gaussiana.

De ello se deduce intuitivamente que, a medida que las cosas convergen hacia distribuciones normales, "quieren" seguir siendo distribuciones normales, ya que su "gaussianidad" se mantiene en muchas operaciones.

Por supuesto, no todo es tan sencillo como una simple tirada de dado, ni tan complejo como la determinación de la altura de un ser humano. Así que hay un gran número de distribuciones que se parecen a una campana, pero que si se examinan con detenimiento no son la distribución normal. Algunos existen en la naturaleza y algunos encuentran aplicación como herramientas matemáticas para algún fin . Mirando a través de Lista de distribuciones de probabilidad de Wikipedia se puede ver que las formas acampanadas son bastante comunes, aunque no sean exactamente la distribución normal.

Pero si combinas estas dos cosas:

• El teorema del límite central significa que la distribución normal es común, y
• muchas distribuciones parecen campanas pero no son la distribución normal,

podría concluir la mayoría de los gráficos de probabilidad muestran una curva de campana .

Answer 2

La convolución de dos funciones es al menos tan bonito como el más bonito de los dos (a menudo incluso más bonito ), y la suma de dos distribuciones independientes tiene una densidad que es la convolución de sus funciones de densidad. Por lo que al convolucionar más y más cuando las sumamos se convierten en más bonito y la función gaussiana es la el más bonito del mundo ¡!

Answer 3

Creo que es importante distinguir entre las curvas generales en forma de campana que no tienen por qué ser normales y la distribución normal. Para esta última, la noción clave, como ya se ha mencionado y elaborado, es el Teorema Central del Límite. A saber, si se cumplen algunas condiciones ligeramente técnicas, las medias y sumas de las muestras convergen (débilmente) a la distribución normal. Sin embargo, $(1)$ no todas las curvas en forma de campana son normales y $(2)$ no todo lo que suponemos normal es realmente normal. Como ya se ha mencionado en los comentarios, muchas variables biológicas no son normales (como la altura y el peso de los seres humanos), pero tienen forma de campana y pueden aproximarse con gran precisión mediante la distribución de Gauss. La misma relación se puede encontrar con la distribución exponencial como un modelo para la duración de la vida de la máquina o algo así - que definitivamente no son realmente exponencial como la máquina no puede "vivir" para siempre.

Por ello, quizá un modelo mejor sean las distribuciones truncadas. Por ejemplo, las alturas pueden describirse bien mediante una distribución normal truncada de dos lados. Pero, ¿cuáles son los problemas en este caso? $(1)$ Si los valores de truncamiento (parámetros) son desconocidos, hay que estimarlos, y $(2)$ además puede introducir mucha más complejidad en tus cálculos. Así pues, la cuestión básica en la modelización estadística (en mi opinión) no es "si tal o cual variable sigue la distribución normal", sino si la variable aleatoria gaussiana puede darnos una buena aproximación de su distribución. Tomemos como ejemplo la estatura de los varones adultos sanos de Escandinavia. Un buen modelo para la distribución de su estatura sería probablemente $N(187, 10)$ pero un modelo más preciso será la misma distribución Normal pero truncada en $5$ desviaciones estándar por encima y por debajo de la media, es decir, fijando el soporte en $[137, 237]$ . Su ganancia en precisión en la estimación de probabilidades es absolutamente despreciable ya que este truncamiento añade menos de $0.001$ a la "masa" de la campana en $[137, 237]$ . La misma lógica se aplica al ejemplo de la duración de la vida de la máquina. Un truncamiento en $\tau$ que está lejos del valor esperado le dará un término de corrección que es $1/P(X<\tau) = 1/(1-e^{-\lambda x})$ e iguala casi $1$ por lo que no obtendrá ningún beneficio práctico.

Otra cuestión que ya se ha mencionado es que la normalidad asintótica no es una verdad universal. N.N. Taleb llamó a la distribución gaussiana "el gran fraude intelectual", con lo que, a mi entender, quería decir que en finanzas el decaimiento exponencial (colas "finas") es una característica muy poco común. Podemos tomar como ejemplo la distribución de Cauchy, que también tiene forma de campana, pero debido a sus colas relativamente "gordas", no tiene una media finita. Esta distribución será una mala aproximación a la altura de los humanos, porque las alturas negativas o los valores "gigantescamente" grandes (digamos, más de $4$ metros) son biológicamente imposibles. Por lo tanto, una distribución de cola gorda que ponga pesos no despreciables en los valores extremos será una modelización matemática inadecuada de dicha variable (altura). Mientras que, en los ingresos puede ser al revés - asumir la normalidad es lo mismo que asumir probabilidades despreciables para ganancias o pérdidas muy grandes, que - como todos sabemos - puede ser simplemente erróneo.

En resumen, parece que la simetría y la forma general de "campana" prevalecen en las distribuciones del mundo real. Sin embargo, la normalidad estricta descrita por $$ f_{X}(x) = \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\}, $$
no es más que una aproximación a la distribución real. Los modelos más precisos que siguen teniendo forma de "campana" pueden ser mejores a la hora de calcular diversos parámetros; sin embargo, la escasa ganancia del modelo más preciso no suele compensar la mayor complejidad que introduce. Por lo tanto, la distribución normal regular sigue siendo en muchos casos no sólo una buena aproximación, sino también muy conveniente. Por último, vale la pena mencionar que hay algunos "dominios" como las finanzas en los que las distribuciones en forma de campana son en su mayoría no normales, y asumir la normalidad en este caso puede ser erróneo.

Answer 4

Como sugieren los comentarios, la respuesta es la Teorema central del límite

En teoría de la probabilidad, el cen que, en la mayoría de las situaciones, cuando independ su suma debidamente normalizada tiende hacia una distribución normal (una normal (una curva de campana) aunque las variables originales no se normales. El teorema es un concepto clave en la teoría de la probabilidad porque implica que los métodos probabilísticos y estadísticos que que funcionan para distribuciones normales pueden aplicarse a muchos problemas que implican otros tipos de distribuciones.

Eso sugiere que las variables independientes naturales en tamaños de muestra razonables tienden a modelar lo que llamamos Distribuciones Normales, o gaussianas.

Answer 5

Intentaré responder a esto con algo de intuición.

La "curva de campana" (en realidad llamada distribución normal) es una distribución de probabilidad que puede observarse en el mundo natural. Son cosas como la distribución de alturas y pesos, donde la mayoría de las personas se sitúan en el medio, con menos ocurrencias en los extremos superior e inferior. ¿Cuántas personas de 1,65 m conoces? ¿Y de 1,80? ¿4 pies y 11 pulgadas?

Como menciona @Chappers, el "Teorema Central del Límite" es una explicación clave. A grandes rasgos (muy a grandes rasgos), este teorema dice que si repites un experimento una y otra vez, la distribución de medias seguirá esta distribución normal.