
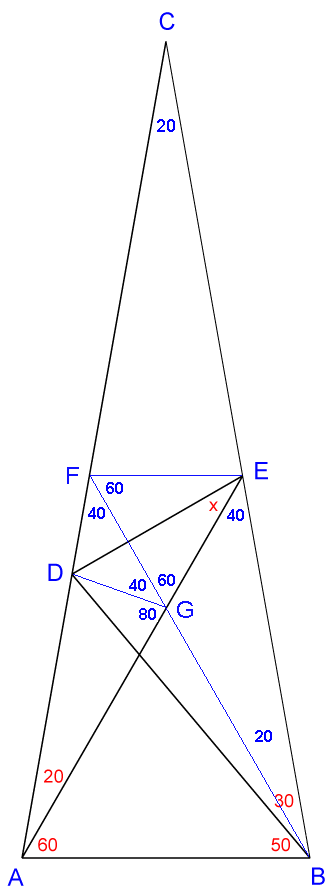
Llegué $x + CBD = 110^{o}$. Creo que debo encontrar las mediciones de ángulo CDB, así que, ¿cómo encontrarlo? ¿Tienes alguna idea? Por favor, ayúdame!

Llegué $x + CBD = 110^{o}$. Creo que debo encontrar las mediciones de ángulo CDB, así que, ¿cómo encontrarlo? ¿Tienes alguna idea? Por favor, ayúdame!
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.