Inconsistencia entre R y SAS de MLE de Weibull

Question

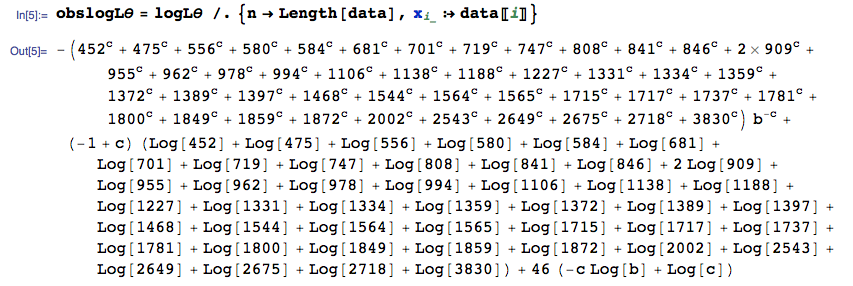
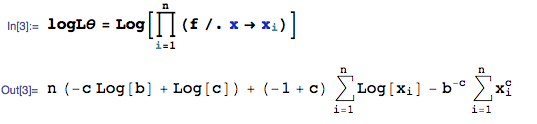Tengo los siguientes datos Y que quiero conseguir un MLE estimación de los parámetros a través de una distribución de Weibull en R.

1468, 1872, 475, 1372, 3830, 1849, 978, 1389, 909, 701, 1227, 962, 1781, 580, 584, 2675, 841, 1544, 452, 955, 556, 1737, 747, 1565, 1331, 1188, 2649, 1800, 2718, 808, 1138, 909, 1359, 846, 1334, 1397, 719, 1715, 681, 2002, 994, 2543, 1564, 1717, 1106, 1859

Si intento ejecutar fitdistr(Y, "weibull") me sale un aviso:

fit = fitdistr(Y, "weibull")
Warning message:
In densfun(x, parm[1], parm[2], ...) : NaNs produced
> warnings(fit)
Warning message:
In densfun(x, parm[1], parm[2], ...) : NaNs produced Error in 
at(list(...), file, sep, fill, labels, append) : 
argument 2 (type 'list') cannot be handled by 'cat'

Pero todavía me da un MLE. Sin embargo, el valor es diferente del resultado SAS da.

la salida de R:

  shape          scale    
 2.1103684   1537.2344072 
(0.2245888)  (112.1596367)

salida de SAS (usando proc lifereg):

 Weibull Scale 1550.559
 Weibull Shape 2.1195

Cuál es la causa de la discrepancia y son los preferidos de los paquetes/funciones para calcular estimaciones sencillas de Emv para las distribuciones más MASS y fitdistr?

Answer 1

Una optimización de la función no deberían dar respuestas idénticas a una función similar en un paquete diferente - o incluso para la misma función con diferentes opciones.

He intentado una variedad de diferentes optimizadores y lugares de partida en fitdistr. Generalmente se le dio muy similares los resultados, de los cuales el SPSS y el resultado que obtuvo con fitdistr en I eran típicos.

He incluido uno de esos ataques, el uso de diferentes optimizador en fitdistr y predeterminada no punto de partida. En términos de la resultante de ajuste, los tres son esencialmente indistinguibles (y sus dos resultados son más parecidos de lo que la tercera):

No creo que algo anda mal.

La advertencia de que no debe ser ignorado, pero investigó la medida de lo posible, pero a veces los errores (o en este caso, advertencias) pueden ser generados sin que indica que hay problemas de convergencia. Usted debe tratar de averiguar lo que hizo. Tratando diferentes puntos de partida y optimizadores (y el trazado de la resultante se ajusta a) se deberá indicar si hay mucho de un problema.

[Idealmente, usted debe graficar la función en un gráfico 3D (o sus contornos en un gráfico 2D) cerca de la identificó óptima, la cual ayudará a identificar una serie de posibles problemas.]

---

Con la de Weibull, una cosa que puede hacer es utilizar la survreg función en el survival paquete que se ajuste a una Weibull como su modelo predeterminado. Sus dos parámetros están relacionados con la costumbre de Weibull (esto se describe en la ayuda en survreg). Lo que desea es una constante-media modelo:

> survreg(Surv(Y)~1)
Call:
survreg(formula = Surv(Y) ~ 1)

Coefficients:
(Intercept) 
   7.354423 

Scale= 0.4703164 

Loglik(model)= -362.2   Loglik(intercept only)= -362.2
n= 46 
> exp(7.354423)   #  exponentiate the Intercept
[1] 1563.095
> 1/0.4703164     #  take inverse of the Scale
[1] 2.126228

summary(survreg) dará errores estándar en la escala que se utiliza, pero si usted toma decir un 95% CI y transformar los extremos, que puede ser utilizado como un IC para la transformación de los parámetros.

Answer 2

Mientras que el SAS de salida es mejor que la salida R, el desagradable hecho es que ambos realizan bastante mal. Para ver esto, observe que el gradiente en el reporte de la solución debe desaparecer a 0 ... mientras que para los del R y SAS resultados, este no es el caso.

En particular, vamos a $X \sim Weibull(b,c)$ con pdf $f(x)$:

Voy a activar mathStaticas' SuperLog función de:

Entonces, la exacta simbólico de la log-verosimilitud para $\theta = (b,c)$ está dada por:

La sustitución de $(x_1, \dots, x_n)$ $n=46$ los valores de los datos de los rendimientos de la exacta observó la log - verosimilitud:

Para el R solución, y la solución de SAS, el vector gradiente, calculados en cada informó la solución, es:

En la solución óptima, el gradiente debería desaparecer a 0. El SAS solución es mejor que la R solución, pero ambos son buenos. La solución reportada por Yves hace mucho mejor:

... pero aún se puede mejorar.

La matriz Hessiana (en la solución) ... y los autovalores de Hesse ... debe ser calculado también para asegurarse de que el observado la log-verosimilitud es cóncava en el barrio.

Answer 3

Primero recordar que el fitdistr (función de la MASA del paquete) es un muy general, función que puede funcionar con casi cualquier distribución. Las advertencias provienen de no permitidos valores de los parámetros (por ejemplo, negativo escala o de forma) se reunió durante la optimización sin restricciones por defecto.

Parece una buena idea para tratar una específica MLE para la Weibull de distribución. Un muy bien conocido el hecho es que la estimación ML de la dos parámetros de Weibull se puede confiar en una concentración de la la log-verosimilitud, que conduce a una más fácil unidimensional la optimización. Por otra parte, la concentración de la log-verosimilitud es cóncava, por lo que no hay una única estimación ML.

El problema aquí es que la log-verosimilitud es bastante plana, cerca de la óptima, de modo que diferentes optimizaciones conducir a resultados diferentes como reportado por @Glen_b. Por otra parte, los datos de escala es propenso a numérico problemas. Después de reescalado, resultados similares se obtienen con o sin concentración. Un general prácticos encontrar cerca de la MLE es que el uso deficiente de los datos a escala puede ser suficiente para arruinar la estimación.

> library(Renext)            ## for concentrated log-lik
> try(fweibull(Y))           ## error (numerical pb with information matrix)
> fit <- fweibull(Y / 1000)  ## works
> ## set parameters and logLik back to original scale
> fit$est * c(1, 1000)
      shape       scale 
   2.126225 1563.094460

> fit$sd * c(1, 1000)
      shape       scale 
  0.2444308 114.1293266

> fit$loglik - length(Y) * log(1000)
[1] -362.2237

> library(MASS)
> ## set parameters and logLik back to original scale
> fit2 <- fitdistr(Y / 1000, "weibull")
> fit2$est * c(1, 1000)
      shape       scale 
   2.126231 1563.095165 

> fit2$sd * c(1, 1000)
      shape       scale 
  0.2288605 114.9071653 

> fit2$loglik - length(Y) * log(1000)
[1] -362.2237