¿BIC o AIC para determinar el número óptimo de clústeres en un gráfico sin escala?

Question

Actualmente estoy tratando de partición de una escala libre ("grande") gráfico (alrededor de 20k vértices, 500k bordes) en los correspondientes sub-gráficos. Deriva el Laplaciano de la gráfica, he intentado correr un enfoque basado en el espectro de vacío y Fiedler-vector, sin embargo, en realidad no inesperadamente, terminó con vértice valoraciones (es decir, los componentes de la correspondiente autovector) estar cerca de cero para una mayoría de los nodos. Claramente, no es obvio corte en el gráfico.

Sin embargo, incluso si es sólo por el bien de mostrar que varios métodos fallan en los gráficos siguientes, las características espectrales de la que estoy trabajando, me gustaría explorar más a fondo espectral enfoques de agrupamiento - algunos de los cuales requieren un fijo k denota el número de particiones.

Soy consciente de que el uso de los BIC y AIC con respecto a k-medios-de la agrupación. Lo que me interesa es, si estos criterios se utilizan también en el ámbito de gráfico espectral agrupación? ¿Hay alguna justificación que permite establecer un vínculo entre los espectros de gráficos de modelo y criterios de selección como el BIC y AIC?

El aporte se agradece mucho!

---

Adiciones:

Así que, he corrido un par de pruebas. He intentado RSB con la mediana para el valor de corte c. He utilizado de alta en la evidencia (baja tasa de falsos positivos, posiblemente a la alta tasa de falsos negativos) clúster de datos para validar contra (aproximadamente ~250 no la superposición de grupos), en un lugar "pobre hombre" de moda, así que nada de lujo en todo. El corte inicial ya ha afectado a más de 235 clusters, aunque muchos de ellos son más bien pequeñas (estamos hablando de un avg. de alrededor de 75 aquí). He intentado apartarse de la mediana por el LOCO (hacia la valoración con el mayor valor absoluto) que resultó en un mal rendimiento. Después de algunos intentos, yo terminé eligiendo el 1er o 3er cuartil de la valoración de la distribución, que permitió a algunos pequeños y bastante trivial cortes. Sin embargo, el espectro de la brecha nunca parecía prometedora, y la característica de valoración simplemente horrible.

Para el cómputo de ellos he utilizado ARPACK (IRLM), así que espero que los resultados sean considerablemente precisos en doble precisión. Aquí está una parcela de la característica de valoración (log2, sólo rápido y sucio) después de las 2 primeras iteraciones (en las que ambos rindieron los 2 grupos de aproximadamente 36 nodos, cada uno) - el núcleo parece ser demasiado denso.

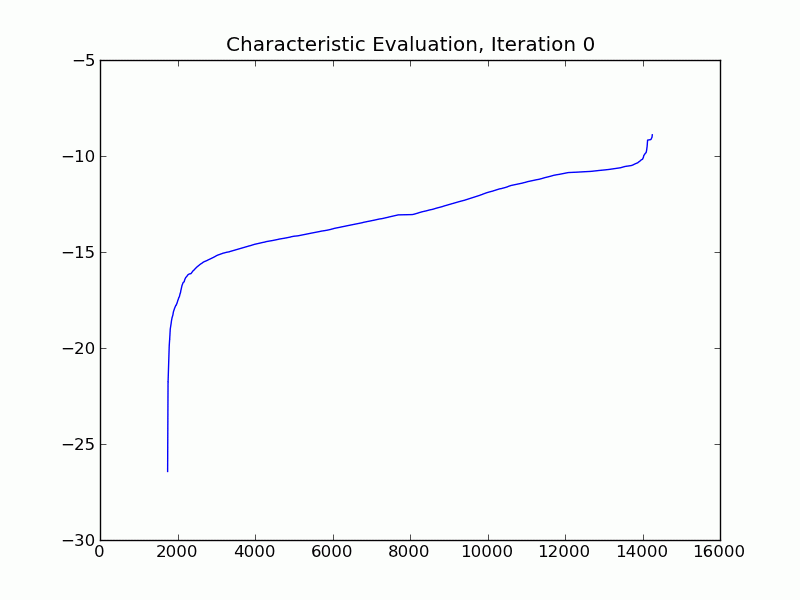
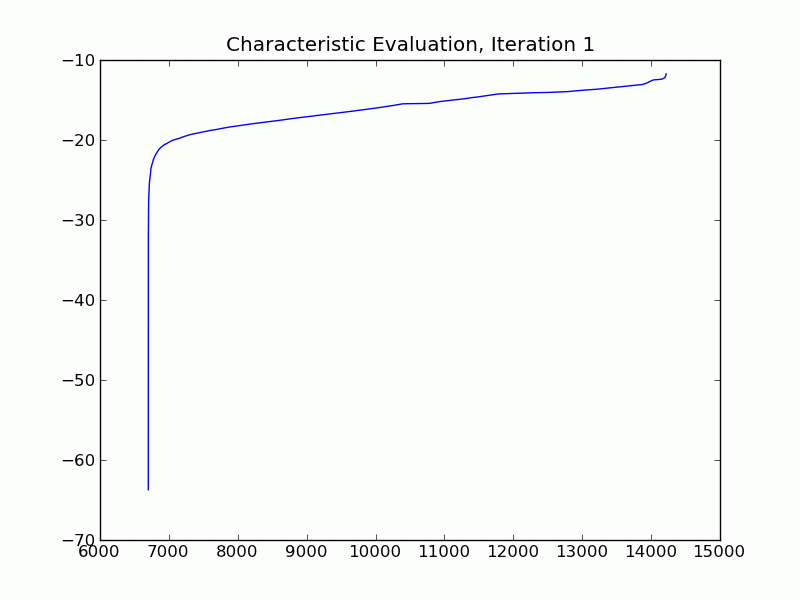
Pensé que por lo menos acerca de la compra de Fan Chung más reciente libro sobre espectral de la agrupación (espectral de la agrupación), desde que me gustó de la lectura a través de la obra anterior (al menos los dos primeros capítulos). Ellos se seca hasta los huesos, pero sin embargo bastante informativa.

Answer 1

AIC y BIC se utilizan para limitar la complejidad de una gama de modelos que compiten para explicar los mismos datos. Tras los pasos de los resultados en la teoría de la complejidad y el aprendizaje de máquina, no hay razón para creer que, en algunos escenarios, el uso de estos proxies para la complejidad da información útil sobre el modelo que explica los datos mejor, mientras que el más pequeño error de generalización.

En este caso, primero sería necesario proponer un modelo que produce la gráfica de los espectros de los que están viendo. Se podría postular que algunos de los diferentes componentes que producen el gráfico se puede ver, como un modelo de mezcla.

Por ejemplo, si usted estaba trabajando con el teléfono de conjunto de datos procedentes de Bélgica (donde hay un trivial de corte para hacer entre aquellos que hablan francés y de los que hablan holandés), sería necesario postular el mecanismo (de preferencia de idioma correlacionada a la región o algo) que en realidad hace que los dos segmentos diferentes de la gráfica.

Luego, una vez que usted tiene un modelo, se haría uso de la AIC o BIC como un medio para optimizar las opciones de los parámetros para el ajuste de la modelo con su observó un gráfico de datos. Si el número de diferentes causales de conglomerados es algo que se incluyen en el modelo, entonces es algo que la optimización de su rutina de escupir de vuelta bajo AIC o BIC restricciones.

Pero no es realmente la misma cosa como normalizado de corte, que no se exactamente el modelo de cualquier cosa sobre el gráfico. Normalizado de la corte (y otros espectral métodos de segmentación) propone una función de coste que pueden o no estar relacionado con nada acerca de su gráfica y, a continuación, hace cortes de manera de minimizar el costo.

Si el costo funcional utilizada por el método de segmentación no de manera significativa corresponden a los aspectos de los datos de generación de proceso que da lugar a su gráfica, entonces la segmentación de rendimiento puede ser arbitrariamente mal. Como usted dice, esta es una razón por la cual uno-tamaño-caber-toda la gráfica de los procedimientos de reducción debe ser utilizado con delicadeza, con una cuidadosa consideración de lo que el coste medio funcional para sus datos.

Tengo un par de fuentes de esto, y voy a volver y el documento que más tarde esta noche.