No recomendaría realmente esta solución, pero me gustaría señalar que también es posible cuando estás realmente atascado. Hay una forma indirecta de encontrar la resistencia equivalente, que es:
-
Apagar todas las fuentes de alimentación independientes. Sustituir las fuentes de voltaje con solo cables (es decir, hacer que dondequiera que estuviera la fuente de voltaje sea un circuito cerrado) y quitar las fuentes de corriente (es decir, hacer que dondequiera que estuviera la fuente de corriente sea un circuito abierto)
-
Conectar una fuente de alimentación de 1V o 1A entre los terminales A y B.
-
Comprobar la salida y usar la ley de Ohm.
Definitivamente no es la mejor opción para esta pregunta, pero resulta útil en ciertas situaciones. Así que aplicando este método aquí, tenemos que
-
Apagar todas las fuentes de alimentación independientes: ya hecho. No hay fuentes de alimentación.
-
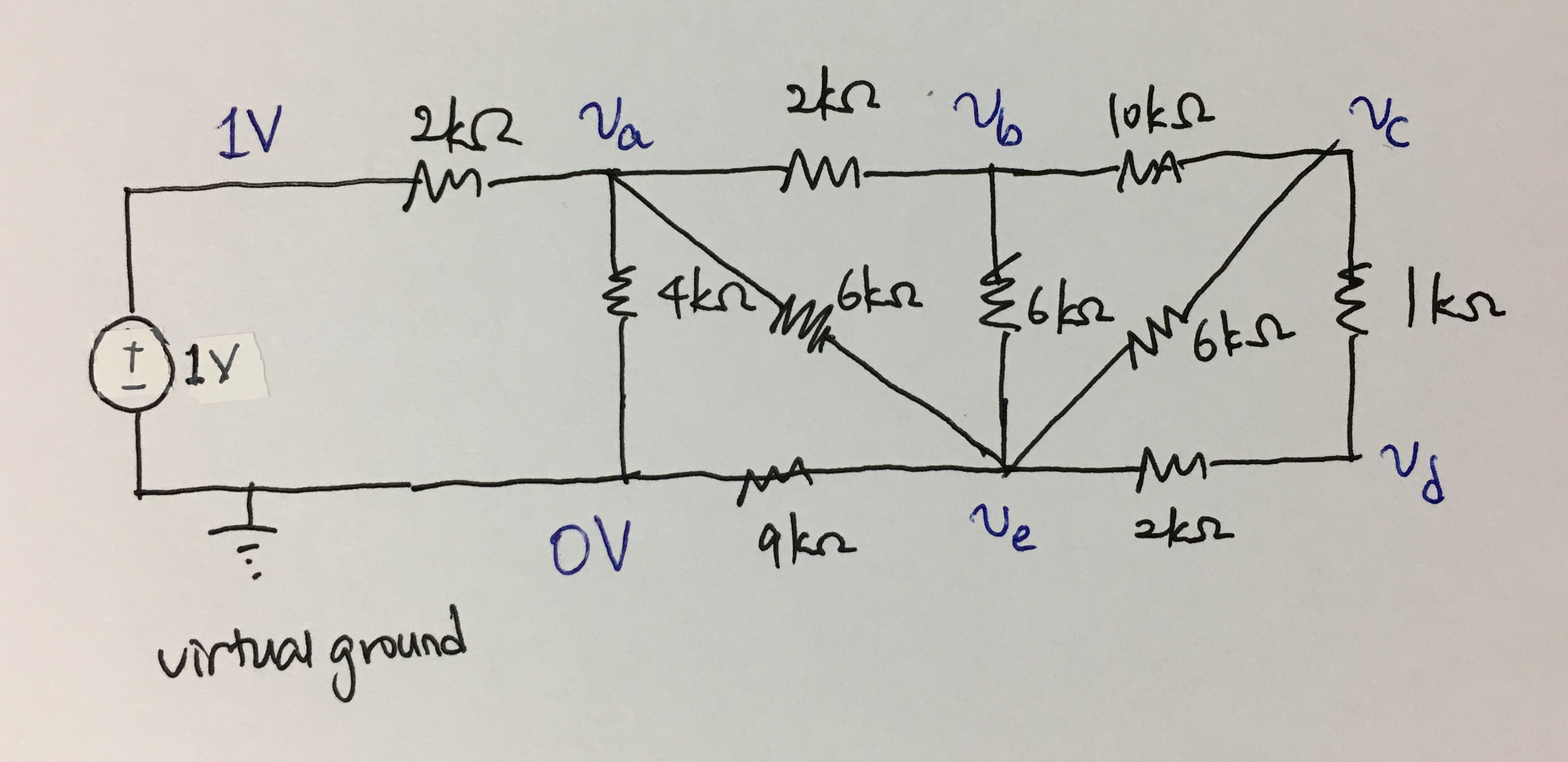
Conectar una fuente de alimentación de 1V:
![]()
- Comprobando la salida: utilizando el análisis de voltaje de nodo, tenemos que: $$ \frac{v_a - 1}{2} + \frac{v_a - 0}{4} + \frac{v_a - v_e}{6} + \frac{v_a - v_b}{2} = 0 $$ $$ \frac{v_b - v_a}{2} + \frac{v_b - v_c}{10} + \frac{v_b - v_e}{6} = 0 $$ $$ \frac{v_c - v_b}{10} + \frac{v_c - v_e}{6} + \frac{v_c - v_d}{1} = 0 $$ $$ \frac{v_d - v_c}{1} + \frac{v_d - v_e}{2} = 0 $$ $$ \frac{v_e - 0}{9} + \frac{v_e - v_a}{6} + \frac{v_e - v_b}{6} + \frac{v_e - v_c}{6} + \frac{v_e - v_d}{2} = 0. $$ Resolviendo la ecuación obtenemos $$ v_a = \frac{3}{5} \mathrm{V}, v_b = \frac{11}{20} \mathrm{V}, v_c = \frac{7}{15} \mathrm{V}, v_d = \frac{83}{180} \mathrm{V}, v_e = \frac{9}{20} \mathrm{V}. $$ Para usar la ley de Ohm y encontrar la resistencia equivalente, básicamente necesitamos conocer la corriente que fluye desde la fuente de voltaje, luego tenemos que \$R = \frac{V}{I}\$, donde \$V= 1 \mathrm{V}\$. Sabemos que la corriente es \$\frac{1 - v_a}{2000} \mathrm{A} = \frac{1}{5000} \mathrm{A}\$. Por lo tanto, \$R = \frac{V}{I} = \frac{1}{\frac{1}{5000}} = 5000 \Omega\$.
Como puedes ver, necesitas hacer algunos cálculos horribles si no tienes una calculadora (y de hecho incluso si la tienes), pero para situaciones en las que la topología parece demasiado complicada para ni siquiera querer intentarlo, esta también es una solución posible.




7 votos
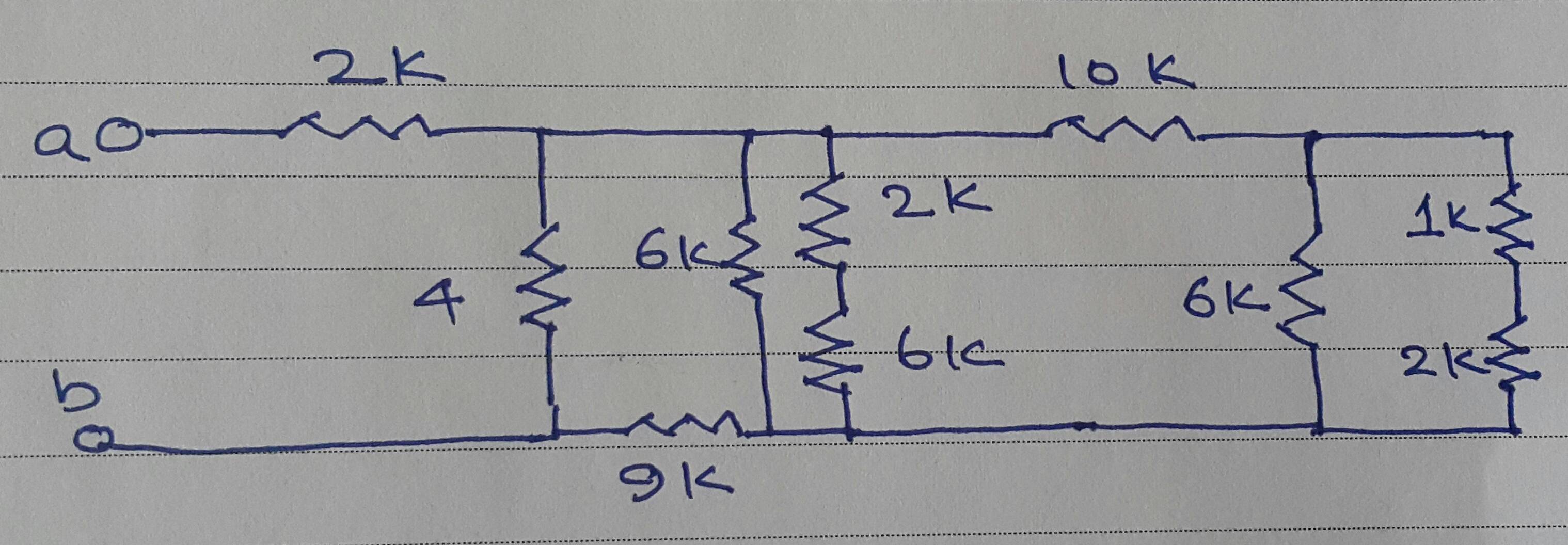
Busca también resistencias en paralelo. Dibuja cada paso simplificado para no cometer errores por accidente.
3 votos
Estas pruebas se supone que sean inconvenientes.... Usa todo lo que sepas.. ¿Cómo te comes un elefante? Una cucharada a la vez.
3 votos
Un ejemplo perfecto de una pregunta de tarea aceptable, bien hecho OP.
3 votos
Puede ser útil si etiquetas las junciones con letras y vuelves a dibujar el circuito con líneas rectas separando las junciones. Mueva 1 junción mientras pivota en otra.
0 votos
(((((((1k+2k)||6K)+10k)||6k)+2k)||6k)+9k)||4k)+2k; comenzar desde el 1k y 2k más a la derecha; + = en serie, || = en paralelo