En primer lugar, no quiero una prueba utilizando $\sin(a+b)=\sin a \cos b + \cos a \sin b$ . En segundo lugar, sospecho que tiene algo que ver con la fórmula de Euler; $e^{ix}=\cos x + i\sin x$ pero no estoy seguro. ¿Puede alguien orientarme? Gracias de antemano.
P.D. Pido disculpas si esta pregunta es un duplicado. No he encontrado ninguna al desplazarme por la lista de "Preguntas que pueden tener ya su respuesta".
La forma más sencilla de obtener/probando esto es a través de la fórmula de Euler:
Tome $e^{i(\theta+\alpha)}$ que, a través de básica exponente reglas sabemos que es igual a $e^{i\theta +i\alpha} = e^{i\theta}\cdot e^{i\alpha}\ .$ Ahora la expansión de este (usando la fórmula de Euler), se obtiene: $$\begin{align} e^{i\theta}\cdot e^{i\alpha} &= (\cos(\theta)+i\sin(\theta))\cdot(\cos(\alpha)+i\sin(\alpha))\\ &= \cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) + i(\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha))\ \\ \end{align}$$ y $$\begin{align} e^{i(\theta + \alpha)} = \cos(\theta + \alpha) + i \sin(\theta + \alpha) \end{align}\ .$$ Recordar que $e^{i(\theta +\alpha)} = e^{i\theta}\cdot e^{i\alpha}\ $podemos ver que $$\cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) + i(\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha))\ = \cos(\theta + \alpha) + i \sin(\theta + \alpha)$$
y porque sabemos que la parte real tiene que ser igual a la parte real y el complejo tiene que ser igual al complejo se obtienen dos ecuaciones: $$\begin{align} \cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) &= \cos(\theta + \alpha)\\ \cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha) &= \sin(\theta + \alpha)\ . \end{align} $$
Ahora nos limitamos a hacer $\alpha = -\phi$, y recuerda que $\sin(-\theta) = -\sin(\theta)$$\cos(-\theta) = \cos(\theta)$, para obtener nuestra resta identidades: $$\begin{align} \cos(\theta - \phi) &=\cos(\theta)\cos(-\phi)-\sin(\theta)\sin(-\phi) \\ &= \cos(\theta)\cos(\phi)+\sin(\theta)\sin(\phi)\\ \\ \sin(\theta -\phi ) &= \cos(\theta)\sin(-\phi)+\sin(\theta)\cos(-\phi) \\ &= -\cos(\theta)\sin(\phi)+\sin(\theta)\cos(\phi)\ \ \blacksquare \end{align} $$
Ahora voy a dar mi favorito de la prueba de esta identidad, que considero que es más intuitiva que la anterior.
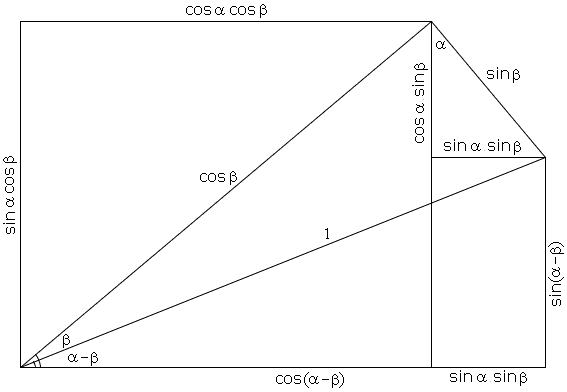
Primero construimos tres triángulos rectángulos, con dos de ellos colocados de manera que la hipotenusa de la primera de ellas es congruente y junto a la base de la otra, y la tercera es construido a partir de la punta superior de la segunda a la base de la primera (perpendicular a ella):
Es claro a partir de esta construcción que estamos buscando la $\sin(\beta + \delta)$, que es igual a $\frac{\overline{DE}}{\overline{DA}}$. Nosotros, sin embargo, quieren poner esto en términos de nuestros primeros dos triángulos, que nosotros probablemente saber más acerca de. Porque la identidad que estamos buscando es en realidad una circular de identidad, o, más bien, es cierto para el círculo unidad, vamos a $\overline{DA}$ ser una radio del círculo unidad (i.e con una medida de $1$). Esto reduce aún más las $\frac{\overline{DE}}{\overline{DA}}$$\frac{\overline{DE}}{1}$, lo $$\sin(\beta + \delta) = \overline{DE}\ .$$
Ahora podemos construir una línea de un punto a a $C$ que es perpendicular a $\overline{DE}$, con el fin de distribuir la línea de $\overline{DE}$:
Ahora podemos decir que debido a $\overline{DE} = \overline{DF} + \overline{FE}$, e $\overline{FE} \cong \overline{CB}$ que $$\sin(\beta + \delta) = \overline{DE} = \overline{DF} + \overline{CB}\ \ .$$
Ahora tratamos de encontrar la $\overline{CB}$ en términos de triángulos sabemos. Porque sabemos que $\sin(\delta) = \frac{\overline{CB}}{\overline{CA}}$ podemos decir que el $\overline{CB} =\sin(\delta)\cdot \overline{CA}$. Ahora podemos tratar de encontrar $\overline{CA}$; notándose que $\cos(\beta) = \frac{\overline{CA}}{DA} $, pero debido a $\overline{DA} = 1$ nos dice $\cos(\beta) = \overline{CA}$, podemos escribir $\overline{CB} =\sin(\delta)\cos(\beta)$. Finalmente, sustituyendo en la ecuación de $\sin(\delta + \beta)$ obtenemos $$\sin(\delta + \beta) = \overline{DF} + \sin(\delta)\cos(\beta)\ .$$
Por último, se debe encontrar $\overline{DF}$, que puede ser escrito en términos del ángulo $\angle FDC$$\cos(\angle FDC) \cdot \overline{DC} = \overline{DF}$. Sabemos que $\angle FDC = 90^{\bigcirc} - \angle DCF$, y sabemos que $\angle DCF = 90^{\bigcirc} - \angle FCA$, así como que $ \angle FCA = 90^{\bigcirc} - \angle ACB$, y, finalmente, que el $\angle ACB = 90^{\bigcirc} - \delta$. Ahora sustituyendo appropriatly llegamos $$\angle FDC = \delta\ .$$ Lo que significa que podemos expresar $\cos(\angle FDC) \cdot \overline{DC} = \overline{DF}$ en términos de delta como sigue $ \overline{DF} = \cos(\delta) \cdot \overline{DC}\ $ Porque sabemos que $\overline{DC} = \sin(\beta)$ podemos decir $$\overline{DF} = \cos(\delta) \cdot \sin(\beta)\ .$$
Sustituyendo en nuestra $\sin(\delta + \beta)$ ecuación obtenemos $$\sin(\delta + \beta) = \cos(\delta)\sin(\beta)+ \sin(\delta)\cos(\beta)\ .$$
Ahora debemos hacer como hicimos en nuestra última prueba y deje $\beta = - \phi$ para obtener $$\begin{align} \sin(\delta -\phi ) &= \cos(\delta)\sin(-\phi)+\sin(\delta)\cos(-\phi) \\ &= -\cos(\delta)\sin(\phi)+\sin(\delta)\cos(\phi)\ \ \blacksquare \end{align} $$
EDIT: me acabo de dar cuenta que no desea que los argumentos que utilizan $\sin(\theta + \alpha)$, por lo que voy a hacer el primer argumento sin $\sin(\theta + \alpha)$.
Tome $e^{i(\theta-\alpha)}$ que, a través de básica exponente reglas sabemos que es igual a $e^{i\theta - i\alpha} = e^{i\theta}\cdot e^{-i\alpha}\ .$ Ahora la expansión de este (usando la fórmula de Euler), se obtiene: $$\begin{align} e^{i\theta}\cdot e^{-i\alpha} &= (\cos(\theta)+i\sin(\theta))\cdot(\cos(-\alpha)+i\sin(-\alpha))\\ &= \cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) + i(\cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha))\ \\ \end{align}$$ y $$\begin{align} e^{i(\theta - \alpha)} = \cos(\theta - \alpha) + i \sin(\theta - \alpha) \end{align}\ .$$ Recordar que $e^{i(\theta - \alpha)} = e^{i\theta}\cdot e^{-i\alpha}\ $podemos ver que $$\cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) + i(\cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha))\ = \cos(\theta - \alpha) + i \sin(\theta - \alpha)$$
y porque sabemos que la parte real tiene que ser igual a la parte real y el complejo tiene que ser igual al complejo se obtienen dos ecuaciones, que simplifican el uso de $\sin(-\theta) = -\sin(\theta)$$\cos(-\theta) = \cos(\theta)$ : $$\begin{align} \cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) &= \cos(\theta + \alpha) &\\ \cos(\theta)\cos(\alpha)+\sin(\theta)\sin(\alpha)&= &\\ \\ \cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha) &= \sin(\theta + \alpha) &\\ -\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha) &=\ &\blacksquare \end{align} $$
Bueno, si compras o tienes acceso a (a través del aprendizaje previo) $e^{i\theta} = \cos \theta + i \sin \theta$ y, a continuación, establecer $\theta = a - b$ uno tiene
$e^{i(a - b)} = \cos(a - b) + i\sin(a - b). \tag{1}$
Pero también,
$e^{i(a - b)} = e^{ia}e^{-ib} = (\cos a + i \sin a)(\cos b - i\sin b). \tag{2}$
La parte imaginaria del producto de la derecha de (20) es $\sin a \cos b - \cos a \sin b$ la parte imaginaria de $e^{(a - b)}$ es $\sin (a - b)$ . Uniendo estas partes imaginarias (es decir, igualándolas) se obtiene
$\sin(a - b) = \sin a \cos b - \cos a \sin b. \tag{3}$
como se iba a demostrar. QED.
Espero que esto ayude. Adiós,
y como siempre,
¡¡Fiat Lux!!
Con los vectores existe una fórmula geométrica para el producto punto
$$\vec{u}\cdot\vec{v}=\left\|\vec{u}\right\|\left\|\vec{v}\right\|\cos\theta$$
donde $\theta$ es el ángulo entre los dos vectores. Tomemos $\vec{u}=\langle\cos(a),\sin(a)\rangle$ y $\vec{v}=\langle-\sin(b),\cos(b)\rangle$ y esta fórmula da
$$\sin(a)\cos(b)-\cos(a)\sin(b)=\cos\theta$$
donde el producto punto se ha calculado utilizando los componentes del vector. Vector $\vec{u}$ puntos $a$ radianes en sentido contrario a las agujas del reloj desde el positivo $x$ -eje. El otro vector, $\vec{v}$ se puede construir tomando el vector $\langle\cos(b),\sin(b)\rangle$ reflejándolo sobre $y=x$ para conseguir $\langle\sin(b),\cos(b)\rangle$ y luego reflexionar sobre $y=0$ para conseguir $\langle-\sin(b),\cos(b)\rangle$ . Teniendo en cuenta cómo afectan estas reflexiones a los ángulos del positivo $x$ -eje, esto hace que $\vec{v}$ El ángulo de la persona es $\pi-\left(\frac{\pi}{2}-b\right)$ que es $\frac{\pi}{2}+b$ .
Así que el valor de $\theta$ es $a-\left(\frac{\pi}{2}+b\right)$ y $$\begin{align} \sin(a)\cos(b)-\cos(a)\sin(b) &=\cos\left(a-\left(\frac{\pi}{2}+b\right)\right)\\ \sin(a)\cos(b)-\cos(a)\sin(b) &=\cos\left(a-b-\frac{\pi}{2}\right)\\ \sin(a)\cos(b)-\cos(a)\sin(b) &=\sin(a-b) \end{align}$$
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
