Hoy estaba pensando en el momento angular orbital y me preguntaba cómo surgen exactamente los números que los cuantizan. Estuve investigando un poco sobre cómo surgen y me encontré con esta imagen muchas veces.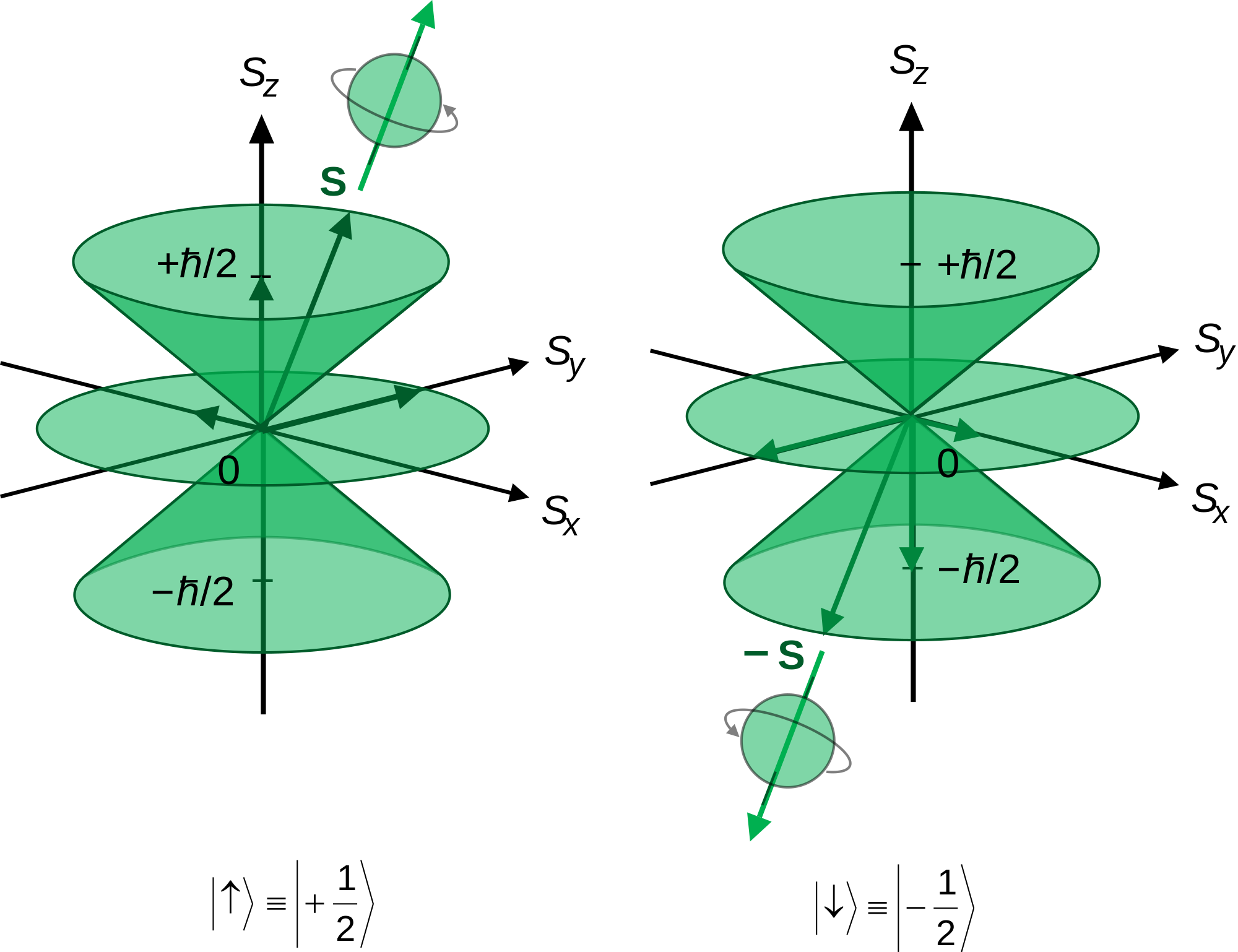 
¿Cómo lo mide exactamente un químico/físico para obtener el número +1/2,-1/2? ¿Hay otros valores posibles?
Respuesta
¿Demasiados anuncios?
$$ \newcommand{\linop}[1]{\hat{#1}} \newcommand{\ramuno}{\mathrm{i}} \newcommand{\ket}[1]{\,|{#1}\rangle} $$
Mecánica clásica
En mecánica clásica, el momento angular , $\vec{L}$ de una partícula respecto a un origen elegido viene dado por el producto vectorial de su vector de posición respecto al origen, $\vec{r}$ y su momento lineal, $\vec{p}$ , \begin{equation*} \vec{L} := \vec{r} \times \vec{p} \, . \end{equation*} Al ampliar $\vec{r}$ y $\vec{p}$ sobre una base estándar $\{ \vec{i}, \vec{j}, \vec{k} \}$ de un sistema de coordenadas cartesianas como $\vec{r} = x \vec{i} + y \vec{j} + z \vec{k}$ y $\vec{p} = p_x \vec{i} + p_y \vec{j} + p_z \vec{k}$ y luego escribir el producto cruzado como el determinante formal [1] y ampliándolo se puede obtener \begin{equation} \vec{r} \times \vec{p} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ x & y & z \\ p_x & p_y & p_z \\ \end{vmatrix} = (y p_z - z p_y) \vec{i} - (x p_z - z p_x) \vec{j} + (x p_y - y p_x) \vec{k} \, , \fin{ecuación} lo que implica que los componentes $(L_x, L_y, L_z)$ del momento angular en términos de los cuales puede expresarse sobre una base estándar como $\vec{L} = L_x \vec{i} + L_y \vec{j} + L_z \vec{k}$ son los siguientes \begin{equation} L_x = (y p_z - z p_y) \, , \quad L_y = (z p_x - x p_z) \, , \quad L_z = (x p_y - y p_x) \, . \end{equation} La magnitud, $L$ del momento angular viene dado, como es habitual, por la raíz cuadrada del producto escalar del vector consigo mismo, $L := \sqrt{\vec{L}\vec{L}}$ o, en términos de componentes, \begin{equation*} L := \sqrt{L_x^2 + L_y^2 + L_z^2} \, . \end{equation*}
Mecánica cuántica
Operadores
El análogo mecánico cuántico del momento angular clásico se conoce como el momento angular orbital y los operadores para las componentes del momento angular orbital pueden obtenerse simplemente sustituyendo las componentes de posición y momento en las expresiones mecánicas clásicas por los operadores correspondientes \begin{equation} \linop{L}_{x} = (\linop{y} \linop{p}_z - \linop{z} \linop{p}_y) \, , \quad \linop{L}_y = (\linop{z} \linop{p}_x - \linop{x} \linop{p}_z) \, , \quad \linop{L}_{z} = (\linop{x} \linop{p}_y - \linop{y} \linop{p}_x) \, . \end{equation} y el cuadrado de la magnitud del operador de momento angular puede expresarse en términos de estos operadores como sigue \begin{equation} \linop{L}^2 = \linop{L}_{x}^2 + \linop{L}_y^2 + \linop{L}_{z}^2 \, . \end{equation} Entonces se pueden establecer fácilmente las siguientes relaciones de conmutación de los operadores de momento angular: \begin{equation} [ \linop{L}_{x}, \linop{L}_{y} ] = \ramuno \hbar \linop{L}_{z} \, , \quad [ \linop{L}_{y}, \linop{L}_{z} ] = \ramuno \hbar \linop{L}_{x} \, , \quad [ \linop{L}_{z}, \linop{L}_{x} ] = \ramuno \hbar \linop{L}_{y} \, , \end{equation} \begin{equation} [\linop{L}^2, \linop{L}_{x}] = [\linop{L}^2, \linop{L}_y] = [\linop{L}^2, \linop{L}_{z}] = 0 \, . \end{equation}
Curiosamente, en mecánica cuántica existe un tipo diferente de momento angular, el momento angular intrínseco o gire que no tiene contrapartida en la mecánica clásica. Aunque los operadores de los componentes del momento angular intrínseco tienen una forma diferente a la del momento angular orbital, las relaciones de conmutación entre ellos y el cuadrado de la magnitud del momento angular intrínseco son exactamente las mismas.
Y lo que es más interesante, el momento angular puede tratarse de tal forma que el tratamiento se base por completo en las relaciones de conmutación que acabamos de introducir, y como tal, válido para cualquier tipo de momento angular. Así, por generalidad podemos utilizar la letra $J$ para cualquier tipo de momento angular reservando la letra $L$ específicamente para la orbital. \begin{equation} [ \linop{J}_{x}, \linop{J}_{y} ] = \ramuno \hbar \linop{J}_{z} \, , \quad [ \linop{J}_{y}, \linop{J}_{z} ] = \ramuno \hbar \linop{J}_{x} \, , \quad [ \linop{J}_{z}, \linop{J}_{x} ] = \ramuno \hbar \linop{J}_{y} \, , \end{equation} \begin{equation} [\linop{J}^2, \linop{J}_{x}] = [\linop{J}^2, \linop{J}_y] = [\linop{J}^2, \linop{J}_{z}] = 0 \, . \end{equation}
Vectores y valores propios
Según las relaciones de conmutación anteriores, $\linop{J}^2$ conmuta con los tres componentes $\linop{J}_{x}, \linop{J}_y, \linop{J}_{z}$ mientras que los componentes no conmutan entre sí. Por lo tanto, $\linop{J}^2$ y uno (y sólo uno) de los operadores componentes, convencionalmente elegido para ser $\linop{J}_{z}$ admiten el conjunto de vectores propios simultáneos, y utilizando la llamada operadores de escalera técnica se puede demostrar que, \begin{align} \linop{J}^2 \ket{j(j+1),m} &= j(j+1) \hbar^{2} \ket{j(j+1),m} \, , \\ \linop{J}_{z} \ket{j(j+1),m} &= m \hbar \ket{j(j+1),m} \, , \end{align} donde $\ket{j(j+1),m}$ es un vector propio simultáneo de $\linop{J}^2$ y $\linop{J}_{z}$ , $j$ puede tomar valores enteros y semienteros no negativos, \begin{equation*} j = 0, 1/2, 1, 3/2, \cdots \, , \end{equation*} y $m$ oscila entre $-j$ à $j$ en pasos enteros \begin{equation} m = -j, -j+1, \cdots, j-1, j \cdots \, . \end{equation}
Entonces, como ya dije en mi comentario con respecto a los valores semienteros de $j$ Para el momento angular orbital, donde la interpretación de Born requiere que se cumplan las condiciones de contorno cíclicas, sólo son admisibles valores enteros, pero donde las condiciones de contorno cíclicas no son relevantes, como para el momento angular intrínseco conocido como espín, los valores semienteros podrían ser apropiados.
Epílogo
Todavía no estoy seguro de qué trata esta pregunta, pero si es específicamente sobre el espín de un electrón, es decir, "¿Cómo sabemos ahora que su componente en cualquier dirección es $\pm 1/2$ en las unidades de $\hbar$ ?", entonces lo sabemos tanto por el experimento ( el de Stern-Gerlach ) y la teoría (el teoría cuántica de campos ). Y sí, para el electrón sólo estos valores son posibles, pero para otras partículas puede haber diferentes posibilidades. Así, por ejemplo, un fotón tiene componente del espín en cualquier dirección $\pm 1$ en las unidades de $\hbar$ .
[1] Aquí, "formal" significa que esta notación tiene la forma de un determinante, pero no se adhiere estrictamente a la definición; es un mnemotécnico utilizado para recordar la expansión del producto cruzado.
