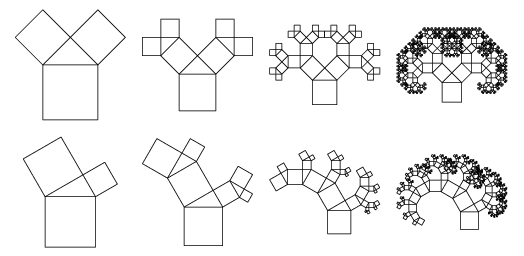
Uno puede calcular el rectángulo delimitador el uso de series geométricas, si $\alpha=\pi/2m$ para algún entero positivo $m$.
Poner en el origen de coordenadas en la esquina inferior derecha de la primera plaza, el nombre de una plaza en posición vertical si sus lados son paralelos a los ejes, se dice que una recta de la plaza se encuentra en la posición $(x,y)$ si su esquina inferior derecha está en esa posición. Deje $\alpha=\pi/2m$ ser el ángulo izquierdo del primer triángulo y establecer$c:=\cos(\alpha)$$s:=\sin(\alpha)$.
Hay una posición vertical cuadrado de lado de longitud $c^m$ en la posición $(-L,H)$ (la plaza más grande en el que la medida de la posición de la izquierda, y el cuadrado más grande que a esa altura), donde
$$
L:=1+\sum_{j=1}^{m-1}c^j \sin(j\alpha)\quad\text{y}\quad H=\sum_{j=0}^{m-1}c^j \cos(j\alpha).
$$
Esta plaza crece a la izquierda, pero de una plaza de sidelength $c^{m-1}s$ en la posición $(-L+c^{m-1}s,H+c^m)=(-L_1,H_1)$ es uno de los dos más grandes plaza en la que la altura y crece hacia arriba y, a continuación, un argumento inductivo muestra que la altura total es
$$
TH=H_1+c^{m-1}s H_1+(c^{m-1})^2 H_1+(c^{m-1})^3 H_1+\dots=\frac{H_1}{1-c^{m-1}}.
$$
Partiendo de la plaza en $(-L,H)$ obtenemos una izquierda obligado a la línea de $x=-TL=-(L+c^m TH)$ y, a continuación, también obtenemos una cota inferior a la línea de $y=LB$ donde
$$
LB=\min\{H_1-c^m TL,0\}.
$$
En el lado derecho obtenemos un cuadrado de sidelength $s^2c^{m-2}$ en la posición $(R+s^2c^{m-2},H_2)$ (que es una de las dos plazas más grandes que la extrema derecha) creciente a la derecha, con
$$
R=-s^2+\sum_{j=0}^{m-2}sc^j \cos((j+1)\alpha)+sc^{m-1}.
$$
A continuación, hay un límite a la derecha en la línea de $y=TR=R+s^2c^{m-2}TH$.
Por lo tanto el más pequeño rectángulo delimitador tiene la altura $|LB|+TH$ y la anchura $TL+TR$.
$\textbf{Examples:}$ Si $m=2$, luego $c=s=\sqrt{2}/2$, $L=1+cs=3/2$, $H=1+c^2=3/2$, $H_1=2$, $TH=\frac{2}{1-cs}=4$,
$TL=3/2+c^2TH=7/2$, $LB=min\{2-7/4,0\}=0$, $R=-s^2+sc+sc=1/2$ y $TR=1/2+2=5/2$, que coincide con el conocido límites para el simétrico del árbol.
Si $m=3$, luego $c=\sqrt{3}/2$, $s=1/2$, $H_1=\frac{17+3\sqrt{3}}{8}$, $TH=\frac{17+3\sqrt{3}}{5}$, $L=1+\frac{5}{8}\sqrt{3}$, $TL=\frac{67+76\sqrt{3}}{40}$, $LB=-\frac{4+81\sqrt{3}}{320}$, $R=\frac{1+3\sqrt{3}}{8}$ y $TR=\frac{7}{20}+\frac{4}{5}\sqrt{3}$.
Por lo tanto el más pequeño rectángulo delimitador tiene la altura $TH+|LB|=\frac{273}{320}(4+\sqrt{3})\approx 4.89$ y la anchura $TL+TR=\frac{27}{40}(3+4\sqrt{3})\approx 6.7$.
En general, para $\alpha =\frac nm \pi$, debería ser posible encontrar la mayor vertical de la plaza y a una cierta altura, lo que le daría la altura, la misma por la extrema izquierda y la extrema derecha cuadrados, lo que le daría el límite inferior y la extensión horizontal del árbol.
Si $\alpha$ no es racional múltiples de $\pi$, el método no funciona, no hay ninguna posición vertical plazas, excepto la primera. Por ejemplo, en el problema 395 mencionado por whatsup en un comentario, el reto es escribir un programa que calcule los límites numéricamente hasta una cierta precisión, por $\alpha=arctan(3/4)$.