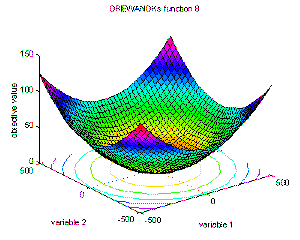
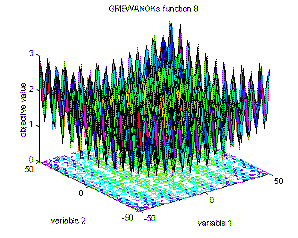
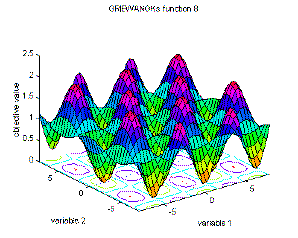
Cada vez que pienso en cómo se comporta una función, siempre trato de identificar un patrón general de comportamiento con algunos números comunes (en algún lugar entre 5 y 100 tal vez) y luego trato de ver si algo interesante sucede alrededor del 1, 0 y en números negativos si corresponde.
Si todo esto funciona, asumo esencialmente que sé que la función se va a comportar de manera similar para números muy grandes como lo hace para esos números relativamente pequeños.
¿Existen funciones notables (famosas, inteligentes o comunes) en las que un número muy elevado de personas haría que se comportaran de manera muy diferente a lo que se pensaría inicialmente si siguiera mi patrón experimental habitual? Si es así, ¿hay alguna señal de advertencia de la que deba ser consciente?