A continuación es una prueba visual (!) que $32.5 = 31.5$. ¿Cómo puede ser eso?
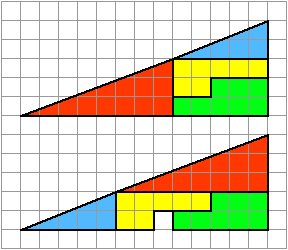
A continuación es una prueba visual (!) que $32.5 = 31.5$. ¿Cómo puede ser eso?

Superposición de los dos triángulos para ver la diferencia. Esto se conoce como la falta de la plaza de puzzle.

Es una ilusión óptica - ni el primero ni el segundo conjunto de bloques que describe, en realidad, un triángulo. El borde diagonal de la primera es ligeramente cóncava y la de la segunda es ligeramente convexo.
A ver con claridad, mira los gradientes de las hipotenusas de los rojo y azul triángulos - que no son "similares".
degradado de azul triángulo de hipotenusa = 2/5
degradado de rojo triángulo de hipotenusa = 3/8
Desde estos gradientes son diferentes, la combinación de ellos en la forma que se muestra en el diagrama no producir general de la recta (en diagonal) de la línea.
Esta cuestión ya ha sido golpeado, y algunas personas encuentran imágenes útiles, como el suministro de ilustraciones de la explicación.
El área del triángulo rojo es $\frac12(8)(3) = 12$ y la de el triángulo azul es $\frac12(5)(2) = 5$. La zona de el amarillo y el verde son las regiones claramente 7 y 8, respectivamente, por lo que el total de área coloreada es 12 + 5 + 7 + 8 = 32, que es menos de 32.5, el área de un 13×5 triángulo. De hecho, en la siguiente figura se puede ver que las hipotenusas de los rojo y azul de los triángulos "dip" por debajo de la real hipotenusa de la gran triángulo; esto representa el 0.5 diferencia en el área.

Del mismo modo, en la segunda figura, la hipotenusa de el rojo y el azul triángulos están por encima de la actual hipotenusa, que representa el 0.5 diferencia en la zona de nuevo.

La diferencia entre las dos figuras es una delgada paralelogramo con vértices en los extremos de las hipotenusas en ambas figuras (de color rosa), que tiene exactamente 1. (Si se ve mucho menos, esa es la naturaleza de la ilusión óptica.)

También, hay algunos enlaces a sitios similares a las cifras del artículo de Wikipedia sobre esta falta de plaza de puzzle.
Sorprendentemente, el caso general sigue siendo ser explicado.
Considerar la recursividad $F(n+2) = F(n+1) + F(n)$, $F(1) = F(2) = 1$
la producción de los números de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ...

Deje que el triángulo azul tiene bordes horizontal y vertical de longitud $F(n+1)$$F(n-1)$, respectivamente.
Deje que el triángulo rojo han horizontal y vertical de los lados de longitud $F(n+2)$$F(n)$, respectivamente.
Así que
en la parte superior de la figura los dos triángulos para crear un rectángulo con un área de $F(n)F(n+1)$
y
en la parte inferior de la figura los dos triángulos para crear un rectángulo con un área de $F(n-1)F(n+2)$
Por Fibonacci identidad $F(n-1)F(n+2) - F(n)F(n+1) = \pm1$
podemos ver que los dos rectángulos están obligados a diferir en el área exactamente en una unidad.
Como n aumenta el gradiente/pendiente de cada triángulo tiende a la plaza de la Proporción áurea $ \phi$,
uno de arriba y otro de abajo.
Por lo tanto, como $\phi^2$ = 0.3819660112...
2/5 = 0.4 > $\phi^2$
3/8 = 0.375 < $\phi^2$
5/13 = 0.3846... > $\phi^2$
etc.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.