Torres en un tablero de ajedrez etiqueta

Question

Una $n\times n$ tablero de ajedrez está estructurada de tal forma que la coordenada $(i, j)$ está etiquetada con $i+j \mod n$.

Ejemplo para n = 6:

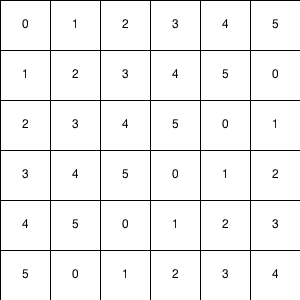
El objetivo es colocar a $n$ torres en el tablero de ajedrez de tal manera que ninguna amenazan unos a otros y que la misma etiqueta nunca se utiliza dos veces.

La solución es trivial para los impares $n$:

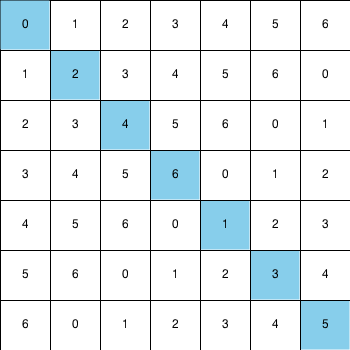
La diagonal siempre puede ser utilizado como torres nunca se amenazan unos a otros a lo largo de una diagonal y todos los números enteros $[0, n)$ será generado en la siguiente entrada de la etiqueta después de $(i, j)$ en la diagonal es $i+1+j+1 = i+j+2 \mod n$, y subiendo a $2\mod n$, por extraño $n$, va a generar todos los números (mirando de $i = j = 0$).

Para todos incluso a $n$, sin embargo, la diagonal no es definitivamente posible. Hay otra solución, aunque? Yo no lo creo, y manualmente intentar generar uno en un consejo siempre parece fallar. Me estoy encontrando muy difícil probar que es imposible, sin embargo.

Ayuda sería muy apreciada! Gracias!

Answer 1

Supongamos que $n$ no atacar Torres han sido colocados en un tablero de ajedrez de $n\times n$ y que $R=\{(i,j)|(i,j){\textrm{ is occupied}}\}$considere $s=\sum_{r\in R}\left((i+j)\mod n\right)$, la suma de las etiquetas de los lugares de $R$, tomado mod $n$. Para que las torres que no atacar, deben haber exactamente una torre en cada fila y en cada columna, así $s \textrm{ mod } n=\left(\sum_{i=0}^{n-1}i+\sum_{j=0}^{n-1}j\right)\!\!\! \mod n = n(n-1)\!\!\! \mod n = 0$. Por lo tanto $s$ divisible en $n$. Si es $n$, $(0+1+\cdots+n-1)$ no es divisible por $n$, por lo que las etiquetas de las plazas ocupadas no se pueden ser $0, 1, 2, \dots, n-1$.