¿Por qué es $\theta \over 2$ utilizada para una esfera de Bloch en lugar de $\theta$?

Question

Soy un principiante en el estudio de la información cuántica, y estoy un poco confundido acerca de la representación de un qubit con una Esfera de Bloch. Wikipedia dice que podemos usar $$\lvert\Psi\rangle=\cos\frac{\theta}{2} \lvert 0\rangle + e^{i\phi}\sin\frac{\theta}{2} \lvert 1\rangle$$ para representar a un estado puro, y el mapa de las coordenadas polares de la esfera. Lo que no estoy seguro es, de dónde viene la "$\frac{\theta}{2}$"?

Quiero decir, en coordenadas polares, el vector es igual a $\cos{\theta}\ \hat{z} + e^{i\phi}\sin{\theta}\ \hat{x}$, pero incluso si utilizamos $\hat{z}=\lvert 0\rangle$$\hat{x}=\lvert 0\rangle + \lvert 1\rangle$, es todavía diferente de la anterior. ¿Cómo podía ser transformado en la fórmula de arriba?

O... ¿significa esto que la esfera es simplemente una representación gráfica de $\theta$$\phi$, mientras que $\lvert 0\rangle$ $\lvert 1\rangle$ no geométricamente corresponde a cualquier vector en la esfera? (pero aquí se escribe $\hat{z}=\lvert 0\rangle$$-\hat{z}=\lvert 1\rangle$...)

Answer 1

I) El punto principal es que la mitad de ángulo $\frac{\theta}{2}$ se duplica cuando se pasa de la cy $$\etiqueta{1} |\psi\rangle~=~\begin{bmatrix}\cos\frac{\theta}{2} \cr e^{i\phi}\sin\frac{\theta}{2}\end{bmatrix}, \qquad ||\psi||~=~1, $$ a la matriz de densidad/operador $$\tag{2}\rho~=~| \psi\rangle \langle\psi | ~=~\frac{1}{2}\left({\bf 1}_{2\times 2}+ \vec{r}\cdot \vec{\sigma}\right),\qquad {\rm tr}\rho~=~1. $$ En eq. (2) $$\tag{3}\vec{r}~=~\begin{bmatrix}x\cr y\cr z\end{bmatrix}~=~\begin{bmatrix}r\cos\phi\sin\theta\cr r\sin\phi\sin\theta\cr r\cos\theta\end{bmatrix},\qquad r~=~1, $$ es el radio vector en coordenadas esféricas, y $\sigma_i$ son las matrices de Pauli. (La mención de la integridad que la esfera de Bloch $S^2=\partial B^3$ de pura qubit de los estados es el límite de la de Bloch balón $B^3$ de mezclado qubit estados.)

II) Alternativamente, para un detallado grupo de explicación teórica de la presencia de la mitad de ángulo, por ejemplo, consultar Ref. 1. En resumen, el 2-dimensional espacio de Hilbert $H\cong\mathbb{C}^2$ de la qubit es un spinor/dublet representación de la $G=SU(2)$ Mentira grupo, que es una doble cubierta de la rotación 3D grupo $SO(3)$. El adjunto de la representación $$\tag{4}{\rm Ad}:~ G ~\longrightarrow~GL(su(2),\mathbb{R}), $$ dada por $$\tag{5} {\rm Ad}(g)\sigma~=~g\sigma g^{-1}, \qquad g~\in~G, \qquad \sigma~\in~su(2)~\cong ~\mathbb{R}^3, $$ es una Mentira grupo homomorphism, cuya imagen $$\tag{6} {\rm Ad}(G)~\cong ~SO(3), \qquad {\rm Ad}(\pm {\bf 1}_{2\times 2})~=~{\bf 1}_{3\times 3},$$ es isomorfo a $SO(3)$. La duplicación de los ángulos implícitamente se lleva a cabo en la fórmula (5). (Esto es similar al hecho de que la mitad de espín de la partícula requiere un $4\pi$ rotación (en lugar de $2\pi$) para volver al punto de partida.)

Referencias:

1. G. 't Hooft, Introducción a la Mentira de los Grupos en Física, notas de la conferencia, en el capítulo 6. El archivo pdf que está disponible aquí.

Answer 2

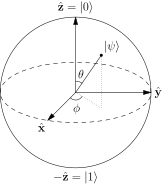
$\newcommand{\ket}[1]{\left|{#1}\right\rangle}$

El $\tfrac{\theta}{2}$ se puede ver en el cuadro que se presenta al final de mi respuesta.

Tal vez usted está confundido porque usted es tentador interpretar $$ \Psi=\cos\frac{\theta}{2} \lvert 0\rangle + e^{i\phi}\sin\frac{\theta}{2} \lvert 1\rangle $$ como una combinación lineal de los vectores en 3D del espacio Euclidiano.

Tenga en cuenta que $\ket{1} \neq -\ket{0}$, contrario a lo que vemos en la esfera de la distancia Euclídea.

Normalmente se define un qubit como un vector en el plano complejo $\mathbb{C}^2$ $$ \Psi = v_0 \cy{0} + v_1 \cy{1} = v_0 \begin{pmatrix} 1 \\ 0 \end{pmatrix}+ v_1 \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} v_0 \\ v_1 \end{pmatrix} $$ donde $v_0$ $v_1$ son complejos los números de satisfacer ${|v_0|}^2+{|v_1|}^2=1$ (a continuación, $\Psi$ se dice que es una normalizado vector). El espacio de qubits tiene dimensión $3$ (escrito $v_k = x_k + {\rm i} y_k$ uno puede comprobar que $(x_0,y_0,x_1,y_1)$ se encuentra en el $3$-dimensional de la esfera de radio $1$ $4$- dimensiones reales espacio Euclidiano).

Pero, al $\Psi$ $\Psi'$ son dos qubits diferentes por un complejo proportionnality factor de $z$ (necesariamente tener el módulo de $1$, luego $z=e^{i\alpha}$, $\alpha$ llama la fase): $$ \Psi' = z \Psi = \begin{pmatrix} zv_0 \\ zv_1 \end{pmatrix} $$ ellos definen la misma "lógica" a través de los Nacidos de la regla (que también significa que $\langle \psi, A\psi\rangle = \langle \psi', A\psi'\rangle$ para la auto-adjunto operadores de $A$), y considerando sólo a los qubits tener forma $$\Psi=\cos\frac{\theta}{2} \lvert 0\rangle + e^{i\phi}\sin\frac{\theta}{2} \lvert 1\rangle \qquad (\star)$$ es suficiente cuando nos fijamos en qubits hasta un complejo proportionnality factor.

Por lo tanto, para los desarrollos teóricos, es suficiente para mirar en la qubits hasta un complejo proportionnality factor, y son llamados los rayos. El espacio de qubits es entonces identificado con el complexe espacio proyectivo $\mathbb{C}\mathbb{P}^1$, y un qubit es identificado con una línea en el plano complejo $\mathbb{C}^2$.

Así que, de hecho, la esfera de Bloch es la representación de $\mathbb{C}\mathbb{P}^1$ como la esfera de Riemann, con la ayuda de la proyección estereográfica $$ \xi = \xi(\Psi) = \frac{v_1}{v_0} = \tan\frac{\theta}{2} e^{i\phi}. $$

La imagen de arriba (tomado de el papel de la Geometría del teorema adiabático) muestra el estado de $\Psi$ sobre la esfera de Riemann correspondiente a la proyección estereográfica $\xi$. Usted puede ver en esta foto donde la $\frac{\theta}{2}$ proviene de. La expresión $(\star)$ $\Psi$ es una combinación lineal en el plano complejo $\mathbb{C}^2$, no en el espacio Euclidiano. Hay dos proyecciones estereográficas que están involucrados aquí: $\xi$ definido anteriormente, cuyo dominio es $\mathbb{C^2}$, y la proyección estereográfica cuyo dominio es la esfera de Riemann. El derecho de los miembros de $(\star)$ no tiene ningún sentido en el espacio Euclidiano, pero el estado $\Psi$ $\mathbb{C}^2$ definido por $(\star)$ tiene la misma proyección estereográfica que el estado $\Psi$ sobre la esfera de Riemann se muestra en la imagen. Esta es la razón por la que nos identifican $\Psi$ como se define por $(\star)$$\Psi$, como se muestra en la imagen.

Answer 3

De la forma es definida $\left| \Psi \right\rangle$ no es un vector en la esfera, sino más bien un vector a lo largo del eje z entre $-\hat{z}$y $\hat{z}$, ya que es una combinación lineal de $\left|0\right\rangle$ y $\left|1\right\rangle$ que son ambos vectores sobre el eje z.

Ahora queremos $\left|\Psi(\theta = 0 , \phi =0)\right\rangle = \left|0\right\rangle$ y $\left|\Psi(\theta = \pi , \phi =0)\right\rangle = \left|1\right\rangle$ $\left|\Psi(\theta , \phi)\right\rangle = \text{cos}\frac{\theta}{2}\left|0\right\rangle + \text{sin}\frac{\theta}{2}e^{i\phi}\left|0\right\rangle$, ya que cos $\frac{\pi}{2}=0$% y sin $\frac{\pi}{2}=1$.