La primera oración de esta página wiki afirma que
En econometría, un problema de endogeneidad ocurre cuando una variable explicativa está correlacionada con el término de error.
Mi pregunta es ¿cómo puede pasar esto? ¿Acaso el beta de regresión se elige de tal manera que el término de error sea ortogonal al espacio de columnas de la matriz de diseño?
Estás confundiendo dos tipos de términos de "error". Wikipedia tiene un artículo dedicado a esta distinción entre errores y residuos.
En una regresión OLS, los residuos (tus estimaciones del término de error o perturbación) $\hat \varepsilon$ están garantizados de ser no correlacionados con las variables predictoras, asumiendo que la regresión contiene un término de intercepción.
Pero los "verdaderos" errores $\varepsilon$ podrían estar correlacionados con ellos, y esto es lo que cuenta como endogeneidad.
Para mantener las cosas simples, considera el modelo de regresión (que podrías ver descrito como el "proceso generador de datos" subyacente o "DGP", el modelo teórico que asumimos para generar el valor de $y$):
$$y_i = \beta_1 + \beta_2 x_i + \varepsilon_i$$
No hay ninguna razón, en principio, por la cual $x$ no pueda estar correlacionado con $\varepsilon$ en nuestro modelo, sin importar cuánto preferiríamos que no violara las suposiciones estándar de OLS de esta manera. Por ejemplo, podría ser que $y$ dependa de otra variable que ha sido omitida de nuestro modelo, y esto se ha incorporado en el término de perturbación (el $\varepsilon$ es donde agrupamos todas las cosas aparte de $x$ que afectan a $y$). Si esta variable omitida también está correlacionada con $x$, entonces $\varepsilon$ a su vez estará correlacionado con $x$ y tendremos endogeneidad (en particular, sesgo por variable omitida).
Cuando estimas tu modelo de regresión en los datos disponibles, obtenemos
$$y_i = \hat \beta_1 + \hat \beta_2 x_i + \hat \varepsilon_i$$
Debido a la forma en que funciona OLS*, los residuos $\hat \varepsilon$ estarán no correlacionados con $x$. Pero eso no significa que hayamos evitado la endogeneidad, simplemente significa que no podemos detectarlo analizando la correlación entre $\hat \varepsilon$ y $x$, que será (hasta error numérico) cero. Y debido a que las suposiciones de OLS han sido violadas, ya no tenemos garantizadas las propiedades agradables, como la imparcialidad, que disfrutamos tanto en OLS. Nuestra estimación $\hat \beta_2$ estará sesgada.
$(*)$ El hecho de que $\hat \varepsilon$ esté no correlacionado con $x$ sigue inmediatamente de las "ecuaciones normales" que usamos para elegir nuestras mejores estimaciones para los coeficientes.
Si no estás acostumbrado al entorno matricial, y me adhiero al modelo bivariado utilizado en mi ejemplo anterior, entonces la suma de los residuos al cuadrado es $S(b_1, b_2) = \sum_{i=1}^n \varepsilon_i^2 = \sum_{i=1}^n (y_i-b_1 - b_2 x_i)^2$ y para encontrar el óptimo $b_1 = \hat \beta_1$ y $b_2 = \hat \beta_2$ que minimizan esto encontramos las ecuaciones normales, primero la condición de primer orden para la intercepción estimada:
$$\frac{\partial S}{\partial b_1} = \sum_{i=1}^n -2(y_i-b_1 - b_2 x_i) = -2 \sum_{i=1}^n \hat \varepsilon_i = 0$$
lo que muestra que la suma (y por lo tanto el promedio) de los residuos es cero, por lo que la fórmula para la covarianza entre $\hat \varepsilon$ y cualquier variable $x$ se reduce a $\frac{1}{n-1} \sum_{i=1}^n x_i \hat \varepsilon_i$. Vemos que esto es cero considerando la condición de primer orden para la pendiente estimada, que es
$$\frac{\partial S}{\partial b_2} = \sum_{i=1}^n -2 x_i (y_i-b_1 - b_2 x_i) = -2 \sum_{i=1}^n x_i \hat \varepsilon_i = 0$$
Si estás acostumbrado a trabajar con matrices, podemos generalizar esto a la regresión múltiple definiendo $S(b) = \varepsilon' \varepsilon = (y-Xb)'(y-Xb)$; la condición de primer orden para minimizar $S(b)$ en el óptimo $b = \hat \beta$ es:
$$\frac{dS}{db}(\hat\beta) = \frac{d}{db}\bigg(y'y - b'X'y - y'Xb + b'X'Xb\bigg)\bigg|_{b=\hat\beta} = -2X'y + 2X'X\hat\beta = -2X'(y - X\hat\beta) = -2X'\hat \varepsilon = 0$$
Esto implica que cada fila de $X'$, y por lo tanto cada columna de $X$, es ortogonal a $\hat \varepsilon$. Luego, si la matriz de diseño $X$ tiene una columna de unos (lo cual sucede si tu modelo tiene un término de intercepción), debemos tener $\sum_{i=1}^n \hat \varepsilon_i = 0$ para que los residuos tengan suma y promedio cero. La covarianza entre $\hat \varepsilon$ y cualquier variable $x$ es nuevamente $\frac{1}{n-1} \sum_{i=1}^n x_i \hat \varepsilon_i$ y para cualquier variable $x$ incluida en nuestro modelo sabemos que esta suma es cero, porque $\hat \varepsilon$ es ortogonal a cada columna de la matriz de diseño. Por lo tanto, no hay covarianza, y no hay correlación, entre $\hat \varepsilon$ y cualquier variable predictora $x$.
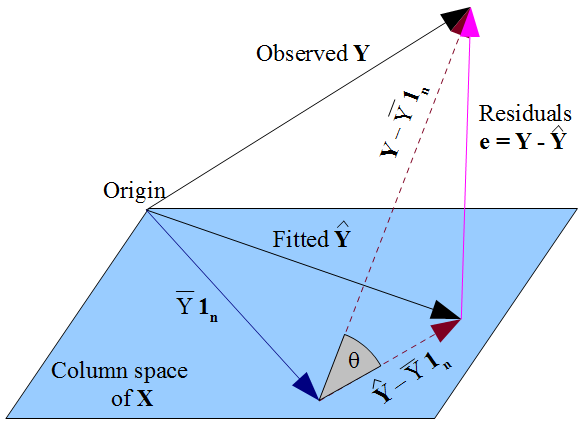
Si prefieres una visión más geométrica de las cosas, nuestro deseo de que $\hat y$ se encuentre lo más cerca posible de $y$ de una manera tipo pitagórica, y el hecho de que $\hat y$ esté restringido al espacio de columnas de la matriz de diseño $X$, dictan que $\hat y$ debería ser la proyección ortogonal del $y$ observado en ese espacio de columnas. Por lo tanto, el vector de residuos $\hat \varepsilon = y - \hat y$ es ortogonal a cada columna de $X$, incluyendo el vector de unos $\mathbf{1_n}$ si se incluye un término de intercepción en el modelo. Como antes, esto implica que la suma de los residuos es cero, por lo que la ortogonalidad del vector residual con las otras columnas de $X$ asegura que no está correlacionado con ninguno de esos predictores.
Pero nada de lo que hemos hecho aquí dice nada sobre los verdaderos errores $\varepsilon$. Suponiendo que hay un término de intercepción en nuestro modelo, los residuos $\hat \varepsilon$ solo están no correlacionados con $x$ como consecuencia matemática de la manera en que elegimos estimar los coeficientes de regresión $\hat \beta$. La forma en que seleccionamos nuestros $\hat \beta$ afecta nuestras valores predichos $\hat y$ y por lo tanto nuestros residuos $\hat \varepsilon = y - \hat y$. Si elegimos $\hat \beta$ por OLS, debemos resolver las ecuaciones normales y estas garantizan que nuestros residuos estimados $\hat \varepsilon$ estén no correlacionados con $x$. Nuestra elección de $\hat \beta$ afecta a $\hat y$ pero no a $\mathbb{E}(y)$ y por lo tanto no impone condiciones sobre los errores verdaderos $\varepsilon = y - \mathbb{E}(y)$. Sería un error pensar que $\hat \varepsilon$ ha "heredado" de alguna manera su falta de correlación con $x$ de la suposición de OLS de que $\varepsilon$ debería estar no correlacionado con $x$. La falta de correlación surge de las ecuaciones normales.
¿Significa que su $y_i = \beta_1 + \beta_2 x_i + \varepsilon_i$ es una regresión con datos de población? ¿O qué significa exactamente?
@user1559897 Sí, algunos libros de texto llamarán a esto la "línea de regresión de la población" o PRL. Es el modelo teórico subyacente para la población; también puedes ver esto llamado el "proceso generador de datos" en algunas fuentes. (Suelo ser un poco cuidadoso al decir que es la "regresión en la población"... si tienes una población finita, por ejemplo, 50 estados de EE. UU., en los que realizas la regresión, entonces esto no es del todo cierto. Si en realidad estás ejecutando una población en algunos datos en tu software, estás hablando realmente de la versión estimada de la regresión, con los "sombreros")
Creo que entiendo lo que estás diciendo. Si te comprendo correctamente, el término de error en el modelo $y_i = \beta_1 + \beta_2 x_i + \varepsilon_i$ también podría tener una expectativa no nula porque es un proceso de generación teórica, no una regresión de mínimos cuadrados ordinarios.
El proceso generador de datos es:
$$ y_i = a + b_1x_{i,1} + b_2x_{i,2} + \epsilon_i$$
Si corriéramos esa regresión, obtendríamos estimaciones $\hat{a}$, $\hat{b}_1$ y $\hat{b}_2$, y con suficientes datos, convergirían en $a$, $b_1$ y $b_2$ respectivamente.
(Nota técnica: Necesitamos un poco de aleatoriedad para no comprar exactamente un pan por cada hamburguesa que compramos en cada visita a la tienda de comestibles. Si hiciéramos esto, $x_1$ y $x_2$ serían colineales.)
Ahora consideremos el modelo:
$$ y_i = a + b_1x_{i,1} + u_i $$
Observa que $u_i = b_2x_{i,2} + \epsilon_i$. Por lo tanto, \begin{align*} \operatorname{Cov}(x_{1}, u) &= \operatorname{Cov}(x_1,b_2x_2 + \epsilon )\\ &= b_2 \operatorname{Cov}(x_{1},x_2) + \operatorname{Cov}(x_{1},\epsilon) \\ &= b_2 \operatorname{Cov}(x_{1},x_2) \end{align*}
¿Es esto cero? ¡Casi con certeza no! ¡La compra de hamburguesas $x_1$ y la compra de pan $x_2$ están casi seguramente correlacionadas! Por lo tanto, $u$ y $x_1$ están correlacionados.
Si intentaras correr:
$$ y_i = \hat{a} + \hat{b}_1 x_{i,1} + \hat{u}_i $$
Tu estimación $\hat{b}_1$ casi seguramente sería una mala estimación de $b_1$ porque las estimaciones de regresión OLS $\hat{a}, \hat{b}, \hat{u}$ se construirían de manera que $\hat{u}$ y $x_1$ no estén correlacionados en tu muestra. ¡Pero el $u$ real está correlacionado con $x_1$ en la población!
¿Qué pasaría en la práctica si hicieras esto? Tu estimación $\hat{b}_1$ del precio de las hamburguesas recogería TAMBIÉN el precio de los panes. Digamos que cada vez que compras una hamburguesa de \$1 tiendes a comprar un pan de \$0.50 (pero no siempre). Tu estimación del precio de las hamburguesas podría ser \$1.40. Estarías recogiendo el canal de la hamburguesa y el canal del pan en tu estimación del precio de la hamburguesa.
Me gusta tu ejemplo de pan de hamburguesa. Explicaste el problema desde la perspectiva de la inferencia estadística, es decir, inferir el efecto de la hamburguesa en el precio. Solo me pregunto cuál sería el efecto si todo lo que me importa es la predicción, es decir, el MSE de predicción en un conjunto de datos de prueba. La intuición es que no va a ser tan bueno, pero ¿hay alguna teoría para hacerlo más preciso? (esto introduce más sesgo, pero menos varianza, por lo que el efecto general no es evidente para mí.)
@user1559897 Si solo te preocupa predecir el gasto, entonces predecir el gasto usando el número de hamburguesas y estimando $\hat{b}_1$ como alrededor de \$1.40 podría funcionar bastante bien. Si tienes suficientes datos, utilizar el número de hamburguesas y panes sin duda funcionaría mejor. En muestras cortas, la regularización $L_1$ (LASSO) podría enviar uno de los coeficientes $b_1$ o $b_2$ a cero. Creo que estás reconociendo correctamente que lo que estás haciendo en regresión es estimar una función de expectativa condicional. Mi punto es que para que esa función capture efectos causales, necesitas suposiciones adicionales.
Supongamos que estamos construyendo una regresión del peso de un animal sobre su altura. Claramente, el peso de un delfín se mediría de manera diferente (en un procedimiento diferente y utilizando instrumentos diferentes) al peso de un elefante o una serpiente. Esto significa que los errores del modelo dependerán de la altura, es decir, de la variable explicativa. Podrían depender de muchas maneras diferentes. Por ejemplo, tal vez tendemos a sobreestimar ligeramente los pesos de los elefantes y subestimar ligeramente los de las serpientes, etc.
Así, establecimos que es fácil encontrarnos en una situación en la que los errores están correlacionados con las variables explicativas. Ahora, si ignoramos esto y procedemos con la regresión como de costumbre, notaremos que los residuos de regresión no están correlacionados con la matriz de diseño. Esto se debe a que, por diseño, la regresión fuerza a que los residuos estén no correlacionados. También ten en cuenta que los residuos no son los errores, son las estimaciones de los errores. Por lo tanto, independientemente de si los errores mismos están correlacionados o no con las variables independientes, las estimaciones de errores (residuos) serán no correlacionadas gracias a la construcción de la solución de la ecuación de regresión.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
11 votos
El beta de regresión se elige de tal manera que el residual sea ortogonal al espacio de columnas de la matriz de diseño. ¡Y esto puede dar una horrible estimación del verdadero beta si el término de error no es ortogonal al espacio de columnas de la matriz de diseño! (es decir, si su modelo no cumple con las suposiciones necesarias para estimar consistentemente los coeficientes por regresión).
3 votos
La ortogonalidad del término de error y el espacio de columnas de la matriz de diseño no es una propiedad de tu método de estimación (por ejemplo, regresión por mínimos cuadrados ordinarios), es una propiedad del modelo (por ejemplo, $y_i = a + bx_i + \epsilon_i$).
0 votos
Creo que tu edición debería ser una nueva pregunta porque parece que has cambiado sustancialmente lo que estás pidiendo. Siempre puedes enlazar de vuelta a esta. (Creo que también necesitas expresarlo mejor, cuando escribes "cuál sería el efecto" entonces no está claro el efecto de qué?) Ten en cuenta que hacer una nueva pregunta generalmente atrae más atención, lo cual sería una ventaja para ti en lugar de editar una existente.