Me gustaría entender un gráfico teórico de la propiedad en términos de teoría de grupos. Tengo algunos aburridos gráficos, y algunos prolijo gráficos, todos creados a partir de los grupos, pero no sé cómo decirle a un aburrido grupo de una casa de grupo.
Hay un grupo de la teoría de la formulación de la existencia de un 4-ciclo en el coset gráfico de la conclusión de la amalgama de 2←1→2×2?
Antecedentes: Esta define un coset geometría o coset gráfico para una amalgama.
Dado un grupo G y dos subgrupos de H, K, definir un simple gráfico bipartito Γ cuyo verde vértices son los cosets de H y el rojo los vértices son los cosets de K, y cuyos bordes están entre los cosets que no tienen intersección vacía.
En términos de la teoría de grafos, esto le da un conectada bi-regular gráfico donde el verde de los vértices tienen grado $[H:H\cap K]$ y el rojo los vértices tienen grado $[K:H\cap K]$. G actúa como automorfismos de la gráfica, con H el estabilizador de un verde vértice, K el estabilizador de una red vértice, y H ∩ Kel estabilizador de un borde dirigido.
El caso especial y pregunta: Cuando $[K:H\cap K]=2$ el gráfico Γ es un gráfico de línea de un multi-gráfico Γ' que se encuentra mediante la contratación de un borde rojo por el vértice.
Cuando hace Γ' tiene varias aristas? De manera equivalente, cuando no Γ tiene un ciclo de longitud 4?
Estoy interesado en un bastante tonto caso: K es de orden 2, H es el Klein 4-grupo, H ∩ K = 1, y G es generado por H y K. En breve: G es la conclusión de la amalgama de 2←1→2×2. El bipartito gráfico debe tener dos desplazamientos involutiva automorfismos de la fijación de un verde vértice, un involutiva automorphism la fijación de una red vértice, y el subgrupo generado por los que debe actuar transitivamente sobre el rojo y el verde vértices. Una pregunta anterior le preguntó sobre la conecta simplemente a cubrir el espacio de estos gráficos.
La roja de todos los vértices tienen grado 2, y supongo que es bien sabido que topológicamente estos son muy simples: se acaba de dividir un borde en dos bordes sin cambiar nada en el real de la conectividad. En otras palabras, para encontrar la conecta simplemente a cubrir el espacio de la libre producto, podríamos haber ignorado por completo el subgrupo de orden 2, y a continuación tenemos un ejemplo del árbol correspondiente a la Klein 4-grupo (con rojo los vértices de división de todos los bordes).
El finito de coeficientes son bastante bonitos, pero algunos de ellos son tanto irritante y aburrido: el rojo los vértices son necesarios para distinguir dos bordes entre el mismo verde de vértices (es decir, el gráfico Γ tiene un ciclo de longitud 4, y por lo que la gráfica Γ' tiene un doble filo). Quiero saber de qué se trata el grupo G que los resultados en estos ciclos de longitud 4 en Γ y esta doble los bordes en Γ'.
Ilustrativo ilustraciones: Aquí hay algunas fotos para mostrar la diferencia entre los aburridos donde Γ' tiene varias aristas, y la ordenada donde no. La imagen de la gráfica Γ' se forma a partir de la imagen de la gráfica Γ haciendo caso omiso de los puntos rojos.
Hay un "aburrido" de la gráfica para cualquier número dado de verde nodos: Organizar n verde nodos uniformemente en un círculo y, a continuación, hacer que el polígono regular inscrito. Dividir cada arista (tanto el curvey toma de la circunferencia del círculo y la recta que hacen los inscritos polígono) en la mitad mediante una red de nodos (de un total de $2n$ rojo nodos). Uno puede (1) cambie el círculo interior con el exterior, (2) reflejan la totalidad de la cosa acerca de un diámetro a través de un verde vértice, y (3) reflejar toda la cosa acerca de un diámetro que va a través de una red vértice, dando los tres automorfismos. Datos básicos sobre el diedro grupos muestran que el grupo generado por estos es bi-transitiva.



Sin embargo, hay un par limpio, como dos triángulos inscritos en un círculo:
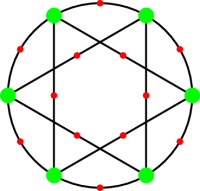


Estas fueron encontradas en los cocientes de la cobertura universal con bajo grado de permutación de las representaciones.
Sería bueno si la respuesta también ayudó a responder a la pregunta:
Que n son tales que no es un buen gráfico n verde vértices (para 2←1→2×2)?


