¿Qué referencias se deben citar para respaldar el uso de 30 como un tamaño de muestra lo suficientemente grande?

Question

He leído/escuchado muchas veces que el tamaño de la muestra de al menos 30 unidades se considera como una "muestra grande" (las suposiciones de normalidad de las medias generalmente se mantienen aproximadamente debido al TCL, ...). Por lo tanto, en mis experimentos, generalmente genero muestras de 30 unidades. ¿Puede usted por favor darme alguna referencia que deba ser citada al utilizar un tamaño de muestra de 30?

Answer 1

En realidad, el "número mágico" 30 es una falacia. Vea el encantador papel de Jacob Cohen, Things I Have Learned (So Far) (Am. Psych. diciembre de 1990 45 #12, pp 1304-1312). Este mito es su primer ejemplo de cómo "algunas cosas que aprendes no lo son tanto".

Uno de mis compañeros candidatos doctorales emprendió una disertación con una muestra de solo 20 casos por grupo. ... Más tarde descubrí ... que para una comparación de medias de dos grupos independientes con $n = 30$ por grupo en el nivel de significancia bidireccional de $.05$, la probabilidad de que un efecto de tamaño mediano fuera etiquetado como significativo por ... una prueba de t era solo $.47$. Por lo tanto, era aproximadamente como lanzar una moneda si se obtendría un resultado significativo, a pesar de que, en realidad, el tamaño del efecto era significativo. ... [Mi amigo] terminó con resultados no significativos, con los cuales procedió a demoler una rama importante de la teoría psicoanalítica.

Answer 2

La elección de n = 30 como límite entre muestras pequeñas y grandes es solo una regla general. Hay una gran cantidad de libros que citan (alrededor de) este valor, por ejemplo, Hogg y Tanis en Probabilidad e Inferencia Estadística (7a edición) dicen "mayor que 25 o 30".

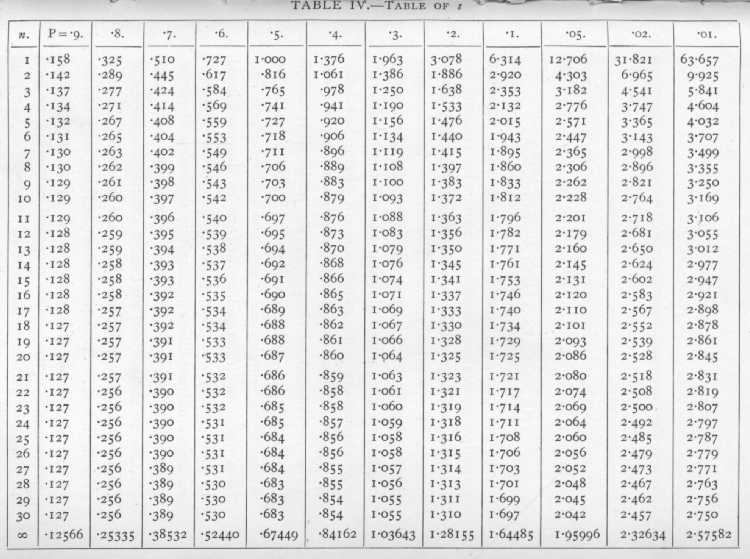
Dicho esto, la historia que me contaron fue que la única razón por la que se consideraba que 30 era un buen límite era porque hacía que las bonitas tablas de Student de t en la parte posterior de los libros encajaran perfectamente en una página. Además, los valores críticos (entre t de Student y Normal) solo difieren aproximadamente hasta 0.25, de df = 30 a df = infinito. Para el cálculo manual, la diferencia realmente no importaba.

Hoy en día es fácil calcular valores críticos con precisión hasta 15 decimales. Además, tenemos métodos de remuestreo y permutación para los cuales ni siquiera estamos limitados a distribuciones poblacionales paramétricas.

En la práctica, nunca confío en n = 30. Grafica los datos. Superpone una distribución normal, si lo deseas. Evalúa visualmente si es adecuada una aproximación normal (y pregúntate si realmente se necesita una aproximación). Si estás generando muestras para investigación y se requiere una aproximación, genera un tamaño de muestra suficiente para que la aproximación sea tan cercana como se desee (o tan cercana como sea factible computacionalmente).

Answer 3

Regla general mayormente arbitraria. Esta afirmación depende de una serie de factores para ser cierta. Por ejemplo, en la distribución de los datos. Si los datos provienen de una Cauchy, por ejemplo, incluso 30^30 observaciones no son suficientes para estimar la media (en ese caso, ni siquiera un número infinito de observaciones sería suficiente para que $\bar{\mu}^{(n)}$ converja). Este número (30) también es falso si los valores que extraes no son independientes entre sí (nuevamente, puede suceder que no haya convergencia en absoluto, independientemente del tamaño de la muestra).

Más generalmente, el TCL básicamente necesita dos pilares para sostenerse:

1. Que las variables aleatorias sean independientes: que puedas reordenar tus observaciones sin perder información*.
2. Que las r.v. provengan de una distribución con momentos de segundo orden finitos: lo que significa que los estimadores clásicos de la media y la desviación estándar tienden a converger a medida que aumenta el tamaño de la muestra.

(Ambas condiciones pueden debilitarse en cierta medida, pero las diferencias son principalmente de naturaleza teórica)

Answer 4

En mi opinión, todo depende de para qué quieras usar tu muestra. Dos ejemplos "tontos" para ilustrar lo que quiero decir: Si necesitas estimar una media, 30 observaciones son más que suficientes. Si necesitas estimar una regresión lineal con 100 predictores, 30 observaciones no serán ni de cerca suficientes.

Answer 5

Esto está destinado a complementar la respuesta del usuario1108 que dice que:

Dicho esto, la historia que me contaron fue que la única razón por la que se consideraba a 30 como un buen límite era porque permitía que las tablas de la t de Student en la parte trasera de los libros de texto encajaran perfectamente en una página. Además, los valores críticos (entre la t de Student y la Normal) solo difieren aproximadamente hasta 0.25, de todos modos, desde df = 30 a df = infinito. Para cálculos a mano, la diferencia realmente no importaba.

Investigué un poco sobre este problema y la fuente más temprana que puedo encontrar es el libro de Fisher Métodos Estadísticos para los Investigadores en Ciencias Sociales (1925). Recuerdo que examiné una copia de este texto (puedes ver http://psychclassics.yorku.ca/Fisher/Methods/, por ejemplo) y noté que la siguiente tabla encajaba perfectamente en una página.

Según lo que recuerdo de la lectura del texto, no hay ninguna justificación por qué Fisher decidió detenerse en $n = 30$. Hasta donde sé, la única justificación para esto es que esas tablas encajaban perfectamente en una página en aquel entonces.