Diferentes maneras de llegar con $1+2+3+\cdots +n=\frac{n(n+1)}{2}$

Question

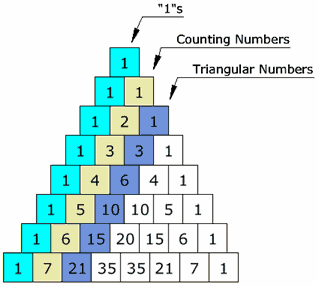
Estoy tratando de compilar una lista de las diferentes maneras de llegar con la forma cerrada para la suma en el título. Hasta ahora tengo el famoso Gauss historia, el argumento contando doubletons, y el uso de funciones de generación. ¿Hay algún otro (de forma significativa) manera diferente de descubrir la forma cerrada?

Para aclarar, de Gauss método fue coger $1+2+3+\dots+n$, escribir al revés, y agregar.

Answer 1

Usted tiene una educación etiqueta así que tal vez usted está buscando una menos rigurosa prueba de que sólo podría tener sentido para los estudiantes.

Si usted tiene los números consecutivos $1,2,3,4,...,n$ a fin de, a continuación, el promedio de los números está en el medio, que es el número más pequeño plus el más grande dividido por $2$.

$\text{average} = \frac{n+1}{2}$

Por supuesto, el principal de la definición de la media es la suma de todos los números dividido por la cantidad de números que hay.

$\text{average} = \frac{1+2+3+4+...+n}{n}$

Igualando estas dos:

$\frac{1+2+3+4+...+n}{n} = \frac{n+1}{2}$

Y por lo tanto

$1+2+3+4+...+n = n\frac{n+1}{2}$

Answer 2

Uno significativamente diferente método es bulldozer a través de la de Euler-Maclaurin fórmula:

$$\sum_{k=1}^nk=\int_0^nx\ dx+\frac12n+c=\frac12n^2+\frac12x+c$$

para algunas constantes $c$. Conectar $n=1$ revela que $c=0$, por lo que

$$\sum_{k=1}^nk=\frac12n^2+\frac12n$$

---

También se puede probar el hockey stick de identidad:

$$\sum_{k=1}^nk=\sum_{k=1}^n\binom k1=\binom{n+1}2=\frac{n(n+1)}{2!}$$

(a los pobres a obtener un cojo nombre) Como se puede ver, cada diagonal es la suma de los anteriores debido a la forma de triángulo de Pascal se hace.

---

Muchos más métodos para calcular esta suma puede ser encontrado en una de mis preguntas favoritas:

Métodos para calcular los $\sum_{k=1}^nk^p$ sin Faulhaber la fórmula de

Answer 3

Quiero añadir esta prueba porque es muy interesante, pero quiero ser claro, indicando que el mérito es de el usuario @SimplyBeautifulArt en este post:

Si sabía de la serie geométrica, usted sabe que

$$\frac{1-r^{n+1}}{1-r}=1+r+r^2+r^3+\dots+r^n$$

Si diferenciamos ambos lados, tenemos

$$\frac{nr^{n+2}-(n+1)r^{n+1}+r}{(1-r)^2}=1+2r+3r^2+\dots+nr^{n-1}$$

Dejando $r\to1$ y aplicando la regla de L'Hospital de la fracción, terminamos con

$$\frac{n(n+1)}2=1+2+3+\dots+n$$

Answer 4

La diferencia de la ecuación de $f(n) - f(n - 1) = n, f(0) = 0$ da $f(n) = \sum_{x=1}^n x$. La solución de la diferencia, la ecuación es bastante fácil, y muestra que los $f(n) = \frac{n(n + 1)}{2}$.

Answer 5

$f(x)=ax^2+bx+c$

$$f(0)=c=0$$

$$f(1)=a+b=1$$ $$f(2)=4a+2b=2+1=3$$

tenemos

$$4a+2b-2(a+b)=2a=3 -2=1$$ $$2a=1 \rightarrow a=\frac{1}{2}$$ $$b=\frac{1}{2} $$ $$f(x)=\frac{x^2+x}{2}$$