De dimensiones más elevadas de lo analógico a grafos planares?

Question

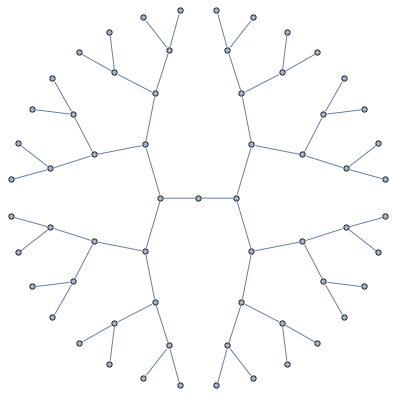
Solemos decir que un grafo es planar si puede ser incorporado en 2-espacio s.t. no hay bordes se cruzan. Aquí está una manera diferente para describir la misma situación: un grafo es planar si puede ser incorporado en 2-espacio s.t. los bordes de la forma de los límites de las células, que en ninguna parte se superponen.

Mi pregunta: se Puede tomar esta segunda definición y extender la idea a las dimensiones superiores? Por ejemplo, permitir que las células se los volúmenes en el espacio de 3 dimensiones - como las burbujas de jabón, donde los bordes del gráfico son la intersección de las películas de jabón paredes.

Answer 1

Un plano gráfico no es otra cosa que una triangulación de la $2$-esfera (a través de la proyección estereográfica), al menos si uno permite arbitraria polígonos en lugar de sólo los triángulos, de manera natural de la generalización a tres dimensiones es triangulaciones de la $3$-esfera, donde se permite arbitraria (convexo) poliedros en lugar de sólo simplices. Uno puede, por supuesto, hablar de las triangulaciones arbitraria de los colectores.

Answer 2

Otra generalización es por el género del eje, es decir, considerar que los gráficos pueden ser incrustados en 2d superficie compacta, como una $n$-toro. Esta área se llama topológico de la teoría de grafos.

Answer 3

No me queda claro acerca de su definición, para un gráfico de abajo, ¿qué son las células y de los límites?