Cuando la inductancia mutua se produce entre dos bobinas, es la auto inductancia siempre se producen en cada individuo de la bobina?

Question

Cuando una bobina conectada a un generador de CA crea una FEM en otro cerca de la bobina (inductancia mutua), es la auto inductancia que ocurren simultáneamente en ambas bobinas?

Answer 1

Cuando una corriente pasa a través de un circuito cerrado, con un flujo magnético a través de la área de la sección transversal de ese bucle surge debido a que los actuales. Este el flujo magnético se relaciona con el actual por la relación:

$$\phi=Li$$

$L$ se llama la auto-inductancia del lazo y depende de la configuración de ese bucle. $L$ se mantiene constante mientras la configuración del bucle no es cambiado.

Si la corriente en el bucle de cambios con el tiempo, el flujo magnético a través de la bucle cambia en proporción a la actual. Este cambio en el flujo magnético causas una fuerza electromotriz (FEM) a ser inducido a través de los terminales del circuito. Este fenómeno se llama auto-inducción. La FEM generada está dada por La ley de Faraday:

$$e=-\dfrac{d\phi}{dt}=-L\dfrac{di}{dt}$$

Un malentendido común en los principiantes es:

Vamos a un voltaje de CA de la fuente de estar conectado a un bucle circular. Como el actual a través del circuito de cambios, hace que el flujo magnético a cambiar. Este cambio en el flujo magnético actúa para cambiar la corriente en el circuito, que luego cambios en el flujo magnético, y así sucesivamente, es decir, somos vueltas en un círculo.

En otras palabras, el cambio en la actual $\rightarrow$ Cambio en el flujo magnético $\rightarrow$ nuevo cambio en la corriente ... el círculo que nunca termina. Este es un concepto erróneo.

Para aclarar cómo se logra el equilibrio, considere la posibilidad de un voltaje aplicado a un ideal (sin resistencia) bucle. Vamos a resolver el circuito mediante la aplicación de KVL. El la tensión aplicada es:

$$V(t)=V_0 \sin(\omega t)$$

Una corriente $I(t)$ establecido en este bucle. El concepto erróneo es que un cambio en $V$ provoca una variación en $I$. Desde $I$ es cambiado, el flujo magnético también cambia, lo que podría provocar la auto-inducción, el cambio de voltaje a través de la red el bucle. Por lo tanto el campo eléctrico existente cambios, de modo que la corriente de nuevo cambio y así sucesivamente. Pero este error tiene un fallo. Por KVL, la suma de los voltajes alrededor del circuito debe ser cero, es decir:

$$V(t)+ \text{induced emf} =0$$

El hecho asombroso es que no es $0$ campo Eléctrico en el interior del alambre de la bucle debido a la resistencia del bucle es $0$. Para un flujo de corriente en un ideal inductor no hay necesidad de $E$. La corriente variable sólo existe para contador de la tensión aplicada.

Sabemos que la FEM inducida se relaciona con el actual en el bucle:

$$e=-\dfrac{d\phi}{dt}=-L\dfrac{di}{dt}$$

Esta relación nos dice que la corriente es una función de la FEM inducida. Desde la FEM inducida es también una función de la tensión aplicada, la corriente es una función de voltaje aplicado y puede ser calculado. Esta es también la expresión de un ideal inductor y la solución es, como sabemos:

$$I(t)=\dfrac{V_0}{\omega L}\cos(\omega t)$$

Esto explica por qué, a pesar de que el círculo de razonamiento, la corriente puede ser encontrado como una función del voltaje aplicado. Esto es debido a que la FEM inducida tiene que ser igual a la tensión aplicada. De hecho, los cambios en las cantidades están relacionadas por una ecuación diferencial cuya solución nos dará el valor de desconocido actual.

Considere dos bucles como se muestra:

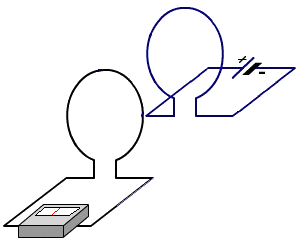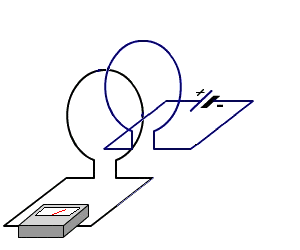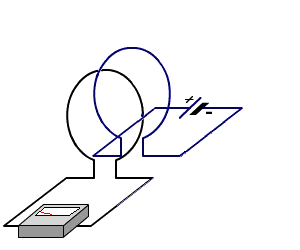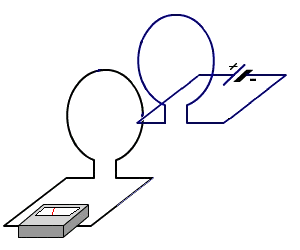
Hay dos bucles, azul y negro. Cuando el negro de bucle no está presente, el la corriente en el lazo azul es $i_1$. Esta corriente es constante y no hay la auto-inducción; la batería tiene un voltaje cero ya que el bucle está perfectamente la realización de. Por el momento, considerar esta batería como un corto circuito.

¿Qué pasa cuando el negro lazo se coloca en las proximidades de la azul bucle? Como el azul del bucle se trasladó a acercarse a la negra de lazo, el flujo magnético a través de tanto el azul y el negro bucles cambiar con el tiempo. Esto produce una FEM inducida a aparecen en ambos bucles. Ambos bucles son ideales conductores, por lo que no necesita ningún $E$ dentro de sus cables a causa de una corriente.

Supongamos que el inicial de la corriente que fluye a través del negro bucle se $i_2$. Ambos $i_1$ $i_2$ va a cambiar cuando los bucles enfoque de cada uno de los otros, pero ¿cómo?

Deja que el azul loop bucle ser$1$ y el negro bucle bucle ser$2$. El flujo magnético cruzando el negro bucle debido a la corriente en el lazo azul es $\phi_{12}(x,t)$. Este flujo está relacionado con a $i_1(t)$ por la ecuación:

$$\phi_{12}(x,t)= M_{12}(x)i_1(t)$$

$M_{12}(x)$ es una función de la distancia $x$ entre los dos bucles y sus de configuración. Este parámetro $M(x)$ se llama inductancia mutua. Si $x$ es no ha cambiado, la inductancia mutua se mantendrá constante.

Del mismo modo, el flujo magnético cruce de bucle$1$ debido a la corriente en el bucle$2$ es:

$$\phi_{21}(x,t)=M_{21}(x)i_2(t)$$

Si ambos bucles tienen la misma configuración, se crea el mismo patrón de campo magnético a su alrededor cuando pasa la misma corriente. Así $M_{12}(x)=M_{21}(x)$ similares bucles y puede ser denominado simplemente como $M(x)$ en que caso.

El flujo magnético existente en el bucle$1$ debido a su propia corriente $i_1$ es:

$$\phi_{11}(t)=L_1i_i(t)$$

El flujo magnético en el bucle$2$ debido a $i_2$ es:

$$\phi_{22}(t)=L_2i_{2}(t)$$

La FEM generada en bucle$1$ y bucle de$2$ son:

$$e_{11}=-\dfrac{d\phi_{11}}{dt}$$ $$e_{22}=-\dfrac{d\phi_{22}}{dt}$$ $$e_{12}=-\dfrac{d\phi_{12}}{dt}$$ $$e_{21}=-\dfrac{d\phi_{21}}{dt}$$

Para KVL para celebrar, la condición es:

$$e_{11}+e_{21}=0=e_{22}+e_{12}$$

Pero $e_{11}$ $e_{22}$ representan la auto-inducción en bucle$1$ y bucle de$2$ respectivly. Por lo $i_1$ $i_2$ tanto varían con el tiempo. Tanto en $\phi_{12}$ y $\phi_{21}$ también va a cambiar debido a los cambios en la $i_1$ $i_2$ y cualquier cambio en $x$. Así podemos simplificar $e_{12}$ como:

$$e_{12}=-\dfrac{d\phi_{12}}{dt} =\dfrac{d(M(x)i_1(t))}{dt} =\dfrac{dM_{12}}{dt}i_1+\dfrac{di_1}{dt}M_{12}$$

$e_{12}$, la FEM inducida en el bucle$2$, es producido por un cambio en x y/o un cambio en el bucle de$1$ actual, $i_1$. Los fenómenos de inducir una fem en un bucle por el cambio de la corriente en algún otro bucle se llama mutuo de la inducción. Si $L_1$ es pequeña, podemos visualizar bucle$1$ como un imán de barra y la auto inducción sólo se observó en bucle$2$. Además, si suponemos que el bucle de$2$ tiene una resistencia $R_2$ muy grande en comparación con $L_2$, vamos a ver nada de auto inducción, sino simplemente La ley de Faraday es decir $e_{12}=i_2R_2$.

Ahora vamos a tratar a su pregunta específica:

"Cuando una bobina conectada a un generador de CA crea una FEM en otra cercana bobina (inductancia mutua), es la auto inductancia que ocurren simultáneamente en ambos bobinas?"

Para analizar esto, considere de nuevo el bucle anterior$1$ y bucle de$2$, en sustitución de la CC de la batería con un voltaje de CA de la fuente. La distancia $x$ entre los bucles no es cambió. Ambos bucles perfectamente llevando a cabo y son comparables auto-inductancias y la igualdad de mutuo-inductancias. Dado que tanto los bucles son ideales los conductores, $E$ dentro de los cables de ambos se $0$.

$$-\dfrac{d(\phi_{11}+\phi_{21})}{dt}+V_0 \sin(\omega t) =0 \implies V_0\sin(\omega t)=L_1\dfrac{di_1}{dt}+M\dfrac{di_2}{dt} \tag{1}$$

También:

$$\dfrac{\phi_{22}+\phi_{12}}{dt}=0 \implies L_2i_2=-Mi_1+k \implies i_2=-M/L_2i_1+k$$

Usando este valor de $i_2$ en la ecuación 1 obtenemos

$$V_0\sin(\omega t)=(L_1-\dfrac{M^2}{L_2})\dfrac{di_1}{dt}$$

Deje ${L_1-\dfrac{M^2}{L_2}}=\alpha$. A continuación, obtenemos una expresión para $i_1$ como:

$$i_1=-\dfrac{V_0}{\omega \alpha}cos(\omega t)$$

Vemos a $i_1$ varía con el tiempo y, por tanto, $i_2$ también por lo tanto los bucles de someterse a la auto-inducción mutua y de la inducción. Este fue un muy condicionada análisis. La resistencia fue ignorado, pero la cosa es aún incluyendo la resistencia la auto-inductancia y la inductancia se va a producir.

Answer 2

Imaginemos dos bobinas de la bobina de la bobina 1 y 2 con la (auto) inductancia $L_1$$L_2$. Si las dos bobinas están no junto, tenemos:

$$v_1 = L_1 \frac{di_1}{dt}$$

$$v_2 = L_2 \frac{di_2}{dt}$$

Ahora, si las bobinas están acoplados, tenemos:

$$v_1 = L_1 \frac{di_1}{dt} + M\frac{di_2}{dt}$$

$$v_2 = M\frac{di_1}{dt} + L_2 \frac{di_2}{dt}$$

donde $M$, la inductancia mutua es dada por

$$M = k\sqrt{L_1L_2}, \, 0 \lt k \le 1 $$

Cuando una bobina conectada a un generador de CA crea una FEM en otro cerca de la bobina (inductancia mutua), es la auto inductancia simultáneamente que ocurren en las dos bobinas?

Primero de todo, tu pregunta es por extraño que sea su enunciado. Obviamente, si uno de los (auto) inductancia es cero, la inductancia mutua es cero en la fórmula de arriba.

Pero, tal vez usted está pidiendo algo más. Si, por ejemplo, la bobina 2 no está conectado a un circuito, a continuación, $i_2$ es cero, por lo que no puede haber auto inducida por tensión.

Sin embargo, no puede ser mutuo, a un voltaje inducido a través de la bobina 2, debido a un cambio de corriente en la bobina 1.

Independientemente, la (auto) inductancias $L_1$ $L_2$ debe ser distinto de cero para allí para ser distinto de cero a la inductancia mutua $M$.

Answer 3

Sí, a veces es insignificante, como en el caso de los dos junto bucle. Pero sería importante por dos bobinas en donde cada uno tiene gran número de vueltas.