Prueba

Question

Este es un seguimiento a esta pregunta. Me encontré con mayor potencial de atado y controlado numéricamente por $0\le x\le 5$. Creo que tiene para todos los positivos $x$, ¿puede alguien ver una prueba?

$$1-\exp(-4x^2/ \pi) \ge \text{erf}(x)^2$$

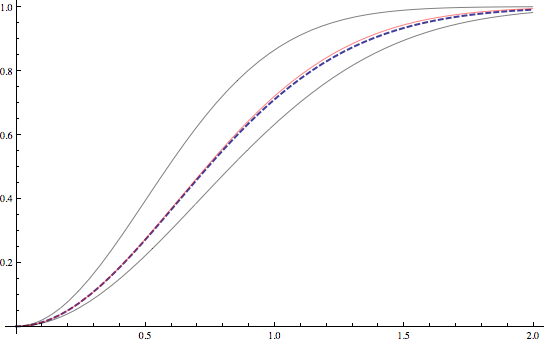
Nota: el uso de análisis para la anterior pregunta se puede demostrar que los $1-\exp(-k x^2)$ es un límite superior en $\text{erf}(x)^2$ $k=2$ y un límite inferior al $k=1$. El factor de $k=4/\pi$ sale cuando numéricamente buscando más apretado el límite superior. No sólo se parecen dar una cota superior, pero también pistas $\text{erf}(x)^2$ muy de cerca.

Discontinua en el gráfico a continuación es $\text{erf}(x)^2$, el rojo es $1-\exp(-k x^2)$$k=4/\pi$, otros dos gráficos son para $k=1$ $k=2$

Answer 1

Como antes de que consideramos

$$erf(x)^2={4\over \pi}\int_0^x\int_0^x \exp{-(s^2+t^2)}\ ds \ dt$$

Ahora Compárelo con el mismo sobre el área que se da por el cuarto de un círculo de radio $\displaystyle \frac{2x}{\sqrt{\pi}}$. El área de este es igual que el área del cuadrado de lado $x$.

Ya que disminuye la $\displaystyle e^{-(s^2 + t^2)}$ $\displaystyle s^2 + t^2$ aumenta, hemos terminado!

La integral sobre el área no común para el círculo cuarto es mayor que la integral sobre el área no-comunes de la Plaza (que se encuentra fuera del círculo y así $\displaystyle s^2 + t^2$ es mayor en esa región).