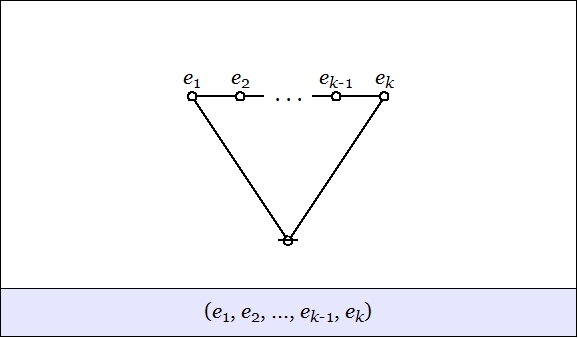
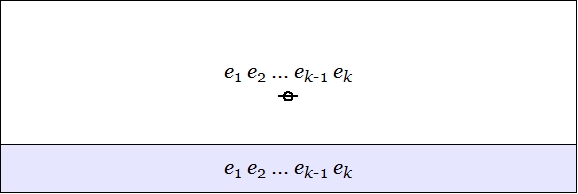Si jugar un poco, probablemente llegado a la misma conclusión que yo hice hace mucho tiempo, a saber, que, efectivamente, hay una verdadera extensión de funciones booleanas $\{0,1\}^n\to \{0,1\}$ a funciones de $[0,1]^n\to [0,1]$. Hay muchas sencillo caracterizaciones de esta extensión (lo cual nos indica que es importante). El más intuitivo para mí es relajarse en la lógica booleana a la probabilidad: tomar de una función booleana de un cierto número de variables, como $$y \text{ or not } (x \text{ and } z).$$ Now suppose we flip possibly biased coins independently to determine the truth values of $x,y,z$. The probability of $x$ being true is $p$, the probability of $s$ being true is $p$, and the probability of $z$ being true is $r$, so we have $0\leq p,q,r \leq 1$. Now consider our expression $y \text{ o } (x \text{ y } z)$: what is the probability that this will be true? It's some function of $p,q,r$ that takes values in $[0,1]$. If you work it out (which is straightforward), you'll find that the function is $$f(p,q,r) = 1-p(1-q)r.$$ You should check that when you restrict $p,q,r$ to be 0 or 1, this agrees with the original boolean function when the corresponding boolean variables are respectively false or true. One of the other main characterizations of this extension is as the unique multiaffine interpolating polynomial. ("Multiaffine" means that if you set all but one of the variables, say $p$, to constant, then you get a linear function $ap + b$ of $p$ for some constants $$ and $b$ (que dependen de las constantes que eligió para el resto de variables)).
Por desgracia, la informática esta extensión para una función booleana de muchas variables es fácilmente visto para ser #P-duro, lo que significa que es uno de los duros problemas que la gente odia porque no se pueden resolver de forma eficiente, pero no puede probar que ellos no pueden. (De hecho, cualquier fácilmente computable representación canónica (que se extiende a [0,1] o de otra manera) aplicable a todas las funciones booleanas podría probar que P=NP, por lo que su problema como se dijo es bastante desesperante. Este particular canónica de la extensión pasa a ser lo suficientemente potente como para ser #P-duro.) Sin embargo, si sus expresiones booleanas tienen sólo unas pocas variables, entonces hay una muy fácil algoritmo recursivo para calcular la extensión. Aquí está:
$$f(p\_1,p\_2,\ldots,p\_n) = p\_1f(1,p\_2,\ldots,p\_n) + (1-p\_1)f(0,p\_2,\ldots,p\_n).$$ $f(1,p\_2,\ldots,p\_n)$ and $f(0,p\_2,\ldots,p\_n)$ are respectively the extensions in which you set the first variable to true and to false, which you can compute recursively. The basis case is when $n=0$, en el que caso de que usted tiene un nullary función 0 o 1.
[Edit: Si su función booleana es en realidad representada, literalmente, como una tabla de verdad, entonces no hay ninguna dificultad en calcular sus canónica de extensión a valores reales; de hecho, el algoritmo recursivo ha dado por encima de $O(N)$ complejidad, donde $N=2^n$ es el número de filas en la tabla de verdad. Por supuesto, la producción de una tabla de verdad para una función de varias variables es el tiempo y el espacio-tiempo, pero si ya tienes la tabla de verdad, entonces usted ya ha comprometido con ella.]
De hecho, hay un caso especial en que la extensión es fácil de calcular, para cualquier número de variables, que puede o no puede ayudar a usted: si usted puede escribir su expresión booleana para cada variable aparece sólo una vez, entonces usted puede calcular la extensión en el tiempo lineal. Utiliza las reglas de transformación
- $(\text{not } A)\to (1-A)$,
- $(A \text{ and } B)\to (AB)$,
- $(A \text{ or } B)\to (A + B - AB)$
y simplemente recurse en la expresión. Mi ejemplo $y \text{ or not } (x \text{ and } z)$ tiene esta propiedad, por lo que vamos a utilizar este procedimiento:
$$ y \text{ or } (\text {not } (x \text{ and } z)) \to y + (1-xz) - y(1-xz), $$ which you can see is the same as $1-x(1-y), z$. This, very unfortunately, fails miserably when you have multiple occurrences of any variable (just try $x \text{ y } x$). However, the situation is just slightly more general than may appear initially: note that I gave transformation rules for AND, OR, and NOT. I did that because it's often convenient to express boolean expressions in terms of those three. You can in fact formulate a corresponding transformation rule for the boolean function $f$ of your choice (which is identical to the canonical extension of $f$: e. g., $1-x$ is the canonical extension of $\text{no }x$ and $x + y - xy$ is the canonical extension of $x\text{ o }y$), and you can apply that transformation to $f(A\_1,\ldots,Un\_n)$ provided that no variable appears in more than one subexpression $\_1,\ldots,\_n$. Por ejemplo, en exclusiva o podría ser una útil función booleana, así que usted puede utilizar la regla de transformación
- $(A \text{ xor } B)\to A + B - 2AB$.
De esta manera, se puede construir una biblioteca de su favorito de funciones booleanas y sus canónica de extensiones, que se puede utilizar como reglas de transformación cada vez que usted aplica las funciones para las subexpresiones con distintos conjuntos de variables.
Por último, permítanme darles una "diversión" para calcular el canónica de extensión según las reglas de transformación que es tremendamente útil cuando computación canónica de la extensión de la mano: resulta que se puede aplicar a cualquier canónica de la transformación de la regla de forma arbitraria, incluso para los argumentos con los no-distintos conjuntos de variables, expanda todo en una suma de monomials, y el uso de la transformación adicional
como tantas veces como puedas hasta que te deja con una multiaffine polinomio. (De hecho, usted es libre de aplicar la transformación, incluso sin la expansión de su polinomio: e. g., $(1 -xy)^2 \to (1-xy)$ es perfectamente válido.) Para ilustrar esto, vamos a aplicar eso a la exclusiva-o de la función:
$$ x \text{ xor } y = (x \text{ or } y) \text{ and not } (x \text{ and } y).$$
Si nos cegamos aplicar las transformaciones Y, O y NO, obtenemos:
$$ x \text{ xor } y \to (x + y - xy)(1-xy). $$ Expandir en monomials:
$$ (x + y - xy)(1-xy) = x + y - xy - x^2y - xy^2 + x^2y^2.$$Now replace $A^2$ by $$ siempre que sea posible:
$$x + y - xy - x^2y - xy^2 + x^2y^2 \to x + y - xy - xy - xy + xy = x + y - 2xy,$ $ , que está de acuerdo con mi canónica de la expresión/transformación de la regla de XOR se indicó anteriormente.