¿Cuál es la distancia más pequeña posible entre dos estrellas?

Question

Si dos estrellas de cualquier tipo se formaran cerca una de la otra, ¿qué tan cerca pueden formarse antes de que algo evite que sean dos estrellas distintas?

Answer 1

Puedes consultar bases de datos de estrellas binarias para saber cuál es el rango de períodos orbitales/separaciones de estrellas en la actualidad. Desafortunadamente, eso no va a responder tu pregunta porque muchos sistemas binarios de corto período han evolucionado de esa manera, por ejemplo, las estrellas variables cataclísmicas de corto período o los binarios de "contacto" conocidos como sistemas W UMa, donde las estrellas realmente se tocan entre sí y tienen una envoltura común. Las binarias también pueden volverse "más compactas" por interacciones con terceros cuerpos, especialmente durante sus vidas tempranas si nacen en cúmulos estelares densos, o las órbitas pueden encogerse o incluso pueden fusionarse debido a la decaimiento orbital inducido por gas durante la fase incrustada temprana de la formación de un cúmulo estelar (Korntreff et al. 2012). Por lo tanto, hay muchos sistemas binarios de período corto más antiguos con períodos más cortos que un día, donde los componentes están apenas separados o ni siquiera separados.

Lo que necesitas hacer es buscar un catálogo de objetos binarios en las regiones más jóvenes de formación estelar o cúmulos estelares, donde podrías asumir razonablemente que ha habido poco tiempo para la interacción (en cierto modo, depende si incluyes la vida temprana en un entorno de formación estelar como parte del proceso de nacimiento o no).

De hecho, es bastante difícil hacer encuestas de este tipo. Necesitas mediciones espectroscópicas repetidas y de alta resolución de objetos bastante tenues para encontrar los corrimientos doppler debido al movimiento binario. Pero hay algunos trabajos por ahí. Meibom et al. (2006) buscan binarios espectroscópicos en los cúmulos jóvenes M34 y M35 (250 y 150 Ma respectivamente). Encuentran 6 binarios en estos cúmulos que tienen separaciones menores a 0.12 ua y períodos inferiores a 13 días. El binario de período más corto tiene un primario de $0.9M_{\odot}$ con un período de 2.25 días. Sin embargo, los autores admiten que estos binarios pueden haber sido compactados por encuentros cercanos con terceros cuerpos.

Morales-Calderon et al. (2012) siguieron un enfoque diferente; realizando monitoreo fotométrico en el infrarrojo para buscar binarios eclipsantes en el muy joven cúmulo de la Nebulosa de Orión (edad aproximada de 2 Ma). Encontraron seis binarios con períodos entre 3.9 y 20.5 días.

Luego hay bastantes otros resultados y estudios individuales. No puedo localizar inmediatamente ninguna buena recopilación, pero esto es lo más cercano a un binario que una búsqueda breve descubrió: Bakis et al. (2011) analizaron el binario IM Mon, probablemente un sistema de 10 Ma de edad en Orión. Encuentran un período orbital de solo 1.19 días y masas primaria y secundaria de 5.5 y 3.3$M_{\odot}$. Sus radios son aproximadamente el 30% de la separación entre los centros estelares (estimada en $a=9.77R_{\odot} = 0.045$ ua). La juventud comparativa y la masa de este binario sugieren que probablemente "nacieron así".

Answer 2

Hay una base de datos de binarios visuales - ese es un buen lugar para empezar. Incluye el siguiente gráfico de periodo y excentricidad:

La esquina inferior izquierda representa un sistema con un periodo de $10^{-1.6}\approx 0.025$ años o un poco más de 9 días.

Ahora, a partir de las leyes de Kepler, tenemos que el cuadrado del periodo escala como el cubo de la distancia promedio. Si las dos estrellas tienen la misma masa que nuestro Sol, podemos estimar la distancia usando la corrección por masa reducida proporcionada en hyperphysics:

$$T^2 = \frac{a^3}{m_1+m_2}$$

donde $a$ se expresa en u.a., $m$ en masa del sol, y $T$ se calcula en años.

Usando esto, terminamos con una distancia estimada de $a = 0.11 u.a.$. Eso está "muy cerca" - mucho más cerca que la órbita de Mercurio. Para referencia, el radio del Sol es 0.0046 u.a. Las fuerzas de marea serían enormes.

Puede haber mejores formas de estimar todo esto - intentaré contactar a algunas personas que saben mucho más sobre estos temas.

Answer 3

Ya hay una respuesta aceptada, pero creo que sería interesante echar un breve vistazo a los procesos físicos que ocurren en estos sistemas.

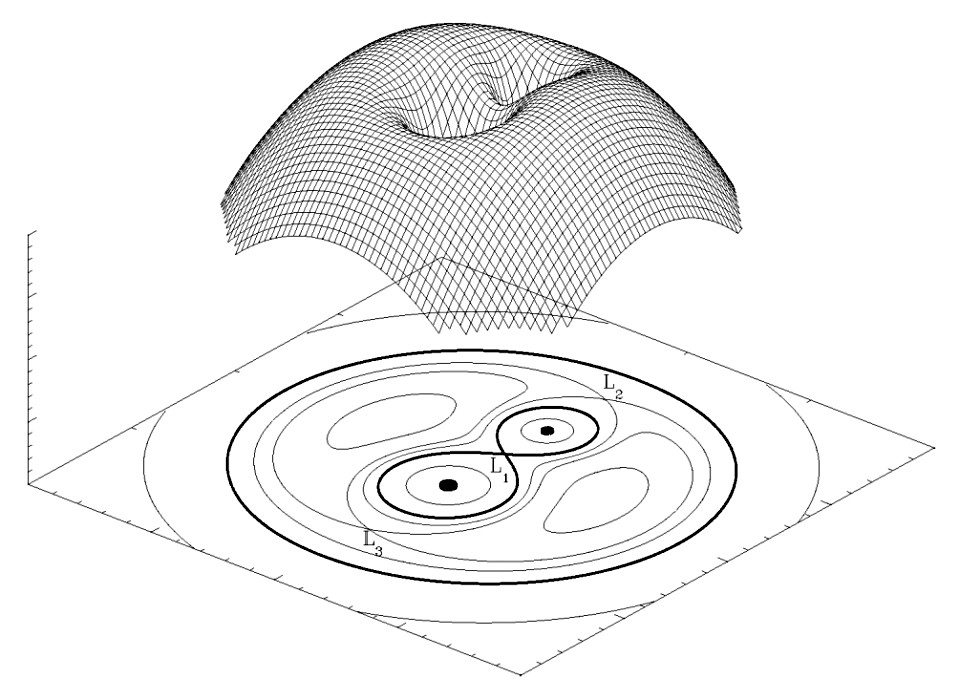
Consideremos primero la mecánica involucrada. Tenemos dos estrellas, en órbita alrededor de su centro de masa, y trabajamos en el marco del centro de masa. Cualquier partícula de prueba en órbita estará sujeta a un potencial debido a la masa de la primera estrella $M_1$, la masa de la segunda estrella $M_2$, y un término para la conservación del momento angular. Esto nos da un potencial: $$\phi = -\frac{GM_1}{r_1}-\frac{GM_2}{r_2} - \frac{1}{2}\omega^2[(x-x_{c.o.m})^2+y^2].$$ La distancia desde el centro de masa a cada estrella se da como $r_1$ y $r_2$. Este es conocido como el potencial de Roche, y es analíticamente un potencial muy desafiante para trabajar. Sin embargo, podemos trabajar con él numéricamente, y eso se muestra a continuación. ¿Qué podemos notar sobre este potencial, aparte del hecho de que se ve bastante feliz? En primer lugar, la fuerza sentida se da por el gradiente del potencial $\nabla \phi$. Podría ser interesante ver los puntos donde una partícula de prueba no siente fuerza, áreas donde el gradiente es cero. Hay 5 de estos puntos, y se llaman puntos de Lagrange. En el diagrama, se muestran 3 de estos, y se marcan como $L_1$, $L_2$ y $L_3. Para el propósito de esta publicación, estamos más interesados en el punto de Lagrange interno$L_1. Aunque para tu interés, como puntos libres de fuerza, son puntos muy útiles para posicionar una nave espacial, por ejemplo, si tienes una sonda para observar el Sol, colocarla en el punto de Lagrange interno entre la Tierra y el Sol te permite siempre mirar al Sol, mientras gastas relativamente poca combustible.

El hecho de que dije relativamente poco me lleva al siguiente punto. Los puntos de Lagrange de 1 a 3 son mínimos inestables. Esto significa que si se perturba ligeramente tu masa de prueba (o tu sonda), saldrá del punto estable. (Los puntos $L_4$ y $L_5$ son mínimos estables, y aun después de una ligera perturbación, la sonda volvería al punto mínimo). Puedes entender esto en términos de una pequeña bola en un tazón de cereal. Si el tazón de cereal está al revés, incluso si mueves un poco la bola desde el centro, volverá al centro. Mientras que si el tazón está boca abajo, mover la bola aunque sea ligeramente hará que se caiga del tazón, y salga del punto estable.

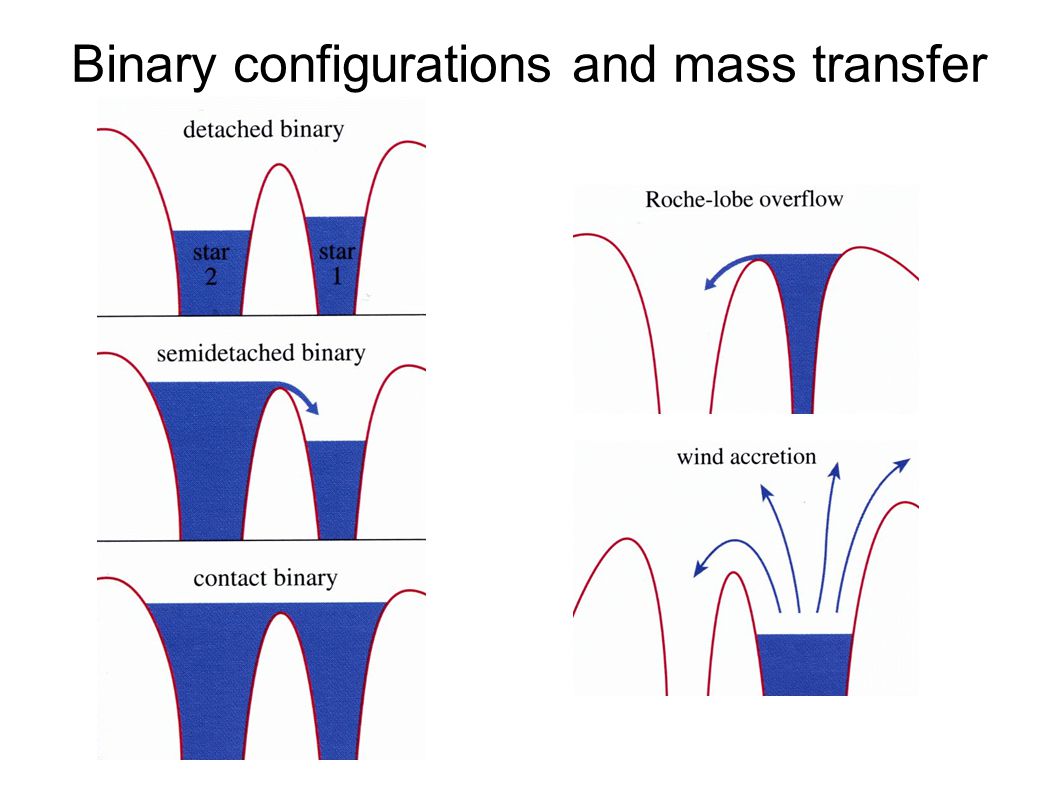
Entonces entre nuestras dos estrellas, tenemos un punto de tazón del revés, donde si la masa de una estrella llega a él, puede caer fácilmente en el potencial de la segunda estrella. Este es un punto tan importante, que definimos los "lóbulos de Roche", como las superficies de $\phi$ constante, que se tocan en el punto de Lagrange interno $L_1$. En el gráfico de contorno, estos son los contornos delineados. Cuando una estrella alcanza su lóbulo de Roche, comienza a distorsionarse en esa forma de gota. (Esta forma distorsionada puede observarse realmente en sistemas binarios, ya que la "cantidad" de estrella que vemos depende de la fase orbital, lo que resulta en una modulación de brillo). Una vez que la estrella alcanza $L_1$, puede comenzar a transferir masa a la otra estrella. En este punto, has alcanzado el tamaño máximo para tu estrella, sin que se convierta en una binaria de contacto. Una idea aproximada de lo que sucede se muestra en el siguiente diagrama:

La estrella que llena su lóbulo de Roche puede transferir masa a la segunda estrella, y es este potencial de Roche el que proporciona un límite físico a dos estrellas que permanecen distintas. Esto sigue siendo una imagen simplista. Puede haber transferencia de masa estable e inestable, dependiendo de $q=M_2/M_1$, la relación de masa. En un caso, a medida que se transfiere la masa, el lóbulo de Roche del donante crece, lo que significa que la estrella ya no está en contacto con su punto $L_1$, evitando la transferencia de masa. En el otro caso, el lóbulo de Roche del donante se contrae, lo que acelera la transferencia de masa. Esta transferencia de masa inestable es entonces un proceso de fuga.

La forma del potencial de Roche depende puramente de $q$, y del período orbital $q$. Luego se escala por $a$, la separación binaria. Eso significa que el límite de la distancia entre dos estrellas distintas dependerá de la distancia de separación binaria, y de la masa de las dos estrellas. Hay varias ajustes numéricos al potencial de Roche, válidos para diferentes rangos de $q$ en tu sistema. Al observar estos, y eligiendo algunos parámetros para tus estrellas, podrías calcular el límite físico real de distancia entre tus estrellas, antes de que ya no puedan considerarse distintas.