Consideremos el siguiente diagrama de Hasse:
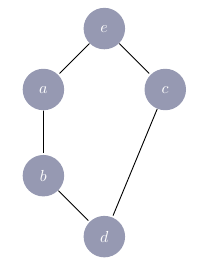
Necesito determinar si esto es una retícula. Según la definición de retícula, puedo probar que la estructura mostrada anteriormente $M_5$ es una retícula si y solo si $\forall x,y \in M_5$, $\{x,y\}$ tiene supremo e ínfimo en $M_5$. Colocando todos esos subconjuntos en una tabla, sin mencionar aquellos subconjuntos donde $x=y$:
$$\begin{array}{|c || c | c|} \hline Subconjunto & x \wedge y & x \vee y \\ \hline \{a,b\} & b & a \\ \{a,c\} & d & e \\ \{a,d\} & d & a \\ \{a,e\} & a & e \\ \{b,c\} & d & e \\ \{b,d\} & d & b \\ \{b,e\} & b & e \\ \{c,d\} & d & c \\ \{c,e\} & c & e \\ \{d,e\} & d & e \\ \hline \end{array}$$
Entonces, $M_5$ es una retícula.
¿Es correcta mi argumentación al detectar supremo e ínfimo para cada subconjunto dado? ¿He llegado a la conclusión correcta?


