Adición : en una nueva respuesta He continuado brevemente la explicación a continuación para definir los tensores generales y no sólo las formas diferenciales (tensores covariantes).
Muchos de nosotros nos confundimos con las nociones de los tensores en la geometría diferencial, no por su estructura algebraica o definición, sino por la confusa notación antigua. La motivación de la notación $dx_i$ está perfectamente justificado una vez que uno se introduce en la diferenciación exterior de las formas diferenciales, que no son más que covectores multilineales antisimétricos (es decir, tomar un número de vectores y dar un número, cambiando de signo si reordenamos sus vectores de entrada). La confusión en tu caso es mayor porque estás usando $x_i$ para su base de vectores, y $x_i$ son en realidad sus funciones de coordenadas locales.
CONSTRUCCIÓN Y NOTACIÓN:
Dejemos que $V$ sea un espacio vectorial finito sobre un campo $\mathbb{k}$ con base $\vec{e}_1,...,\vec{e}_n$ , dejemos que $V^*:=\operatorname{Hom}(V, \mathbb{k})$ sea su espacio vectorial dual es decir, el espacio lineal formado por los funcionales lineales $\tilde\omega: V\rightarrow\mathbb{k}$ que comen vectores y dan escalares. Ahora el producto tensorial $\bigotimes_{i=1}^p V^*=:(V^*)^{\otimes p}$ es sólo el espacio vectorial de las funciones multilineales $\tilde\omega^{(p)}:V^k\rightarrow\mathbb{k}$ Por ejemplo $\tilde\omega (\vec v_1,...,\vec v_k)$ es escalar y lineal en sus vectores de entrada. En alternando esos espacios, se obtienen las funciones multilineales antes mencionadas, que satisfacen $\omega (\vec v_1,...,\vec v_k)=\operatorname{sgn}(\pi)\cdot \omega (\vec v_{\pi(1)},...,\vec v_{\pi(k)})$ para cualquier permutación del $k$ entradas. El ejemplo más sencillo es pensar en vectores fila y matrices: si tus vectores son columnas, piensa que los covectores son vectores fila que por producto matricial te dan un escalar (¡en realidad su típico producto escalar!), se llaman formas únicas; de forma similar cualquier matriz multiplicada por un vector columna a la derecha y por un vector fila a la izquierda te da un escalar. Una matriz antisimétrica funcionaría de forma similar pero con la propiedad de alternancia, y se llama una dos-forma. Esto se generaliza para entradas de cualquier $k$ vectores.
Ahora, curiosamente, sólo hay un número finito de esos espacios alternativos : $$\mathbb{k}\cong V^0, V^*, (V^*)^{\wedge 2}:=V^*\wedge V^*,..., (V^*)^{\wedge \dim V}.$$ Si considera que su $V$ -base para ser $\vec{e}_1,...,\vec{e}_n$ por construcción su espacio dual de covectores tiene una base de la misma dimensión dada por las formas lineales $\tilde e^1,...,\tilde e^n$ que satisfacen $\tilde e^i (\vec e_k)=\delta^i_k$ es decir, son los funcionales que dan $1$ sólo sobre sus vectores duales y $0$ en el resto (los covectores suelen estar indexados por superíndices para utilizar el Convención de suma de Einstein ). Por ello, cualquier covector que actúe sobre un vector $\vec v=\sum_i v^i\vec e_i$ se puede escribir $$\tilde\omega =\sum_{i=1}^n \omega_i\tilde e^i\Rightarrow \tilde\omega(\vec v) =\sum_{i=1}^n \omega_i\tilde e^i(\vec v)=\sum_{i=1}^n \omega_i\cdot v^i.$$
Finalmente, cuando se trabaja en colectores diferenciales, se dota a cada punto $p$ con un espacio tangente $T_p M$ de vectores tangentes y así se obtiene un espacio dual $T_p^* M$ de covectores y su espacio alterno $\Omega_p^1(M)$ de alternancia 1 forma (que en este caso coinciden). De forma análoga, se define el $k$ -sobre los vectores tangentes que definen $\Omega_p^k(M)$ . Como estos espacios dependen de un punto a otro, se empieza a hablar de campos de vectores tangentes y campos de diferencial $k$ -forma que varían en componentes (con respecto a su campo base elegido) de un punto a otro.
Ahora el hecho interesante es que la definición intrínseca constructiva de los vectores tangentes se basa en derivados direccionales en cada punto. Piensa en tu colector $M$ de dimensión $n$ como se da localmente en el gráfico alrededor de un punto $p$ por coordenadas: $x^1,...,x^n$ . Si tiene una curva $\gamma:[0,1]\subset\mathbb R\rightarrow M$ sobre su colector pasando por su punto $p$ de interés, se pueden definir intrínsecamente vectores tangentes a $p$ mirando las derivadas direccionales en $p$ de cualquier función suave $f:M\rightarrow\mathbb R$ que vienen dados por la tasa de cambio de $f$ sobre cualquier curva que pase por $p$ . Es decir, en coordenadas locales su derivada direccional en el punto $p$ a lo largo de (en la dirección tangente de) una curva $\gamma$ que lo atraviesa ( $\gamma(t_0)=p$ ) viene dada por (utilizando la regla de la cadena para la diferenciación con las coordenadas locales para $\gamma (t)$ ): $$\frac{d f(\gamma(t))}{dt}\bigg|_{t_0}= \sum_{i=1}^n\frac{\partial f}{\partial x^i}\bigg|_p\frac{d x^i(\gamma (t))}{d t}\bigg|_{t_0}=\sum_{i=1}^n X^i\vert_p\frac{\partial f}{\partial x^i}\bigg|_p.$$ Así es como debe entenderse esa ecuación: en cada punto $p$ Las diferentes curvas tienen diferentes "vectores tangentes" $X$ con componentes locales $X^i\vert_p\in\mathbb R$ dada por la diferenciación paramétrica de las ecuaciones locales de la curva (por lo que en realidad sólo hay que preocuparse por las clases de equivalencia de las curvas que tienen la misma dirección en cada punto); la derivada direccional en cualquier punto de cualquier función en dirección $X$ es, por tanto, expresable como operador: $$X=\sum_{i=1}^n X^i\frac{\partial}{\partial x^i},$$ para todos los componentes posibles $X^i$ tales que son campos escalares suaves sobre la variedad. De esta manera se ha adjuntado un espacio tangente $T_pM\cong\mathbb R^n$ en cada punto con base canónica $\vec e_i=\frac{\partial}{\partial x^i}=:\partial_i$ para cada gráfico local de coordenadas $x^i$ . Esto parece estar muy lejos de la noción visual de "flecha" de los vectores y vectores tangentes como se ve en las superficies y submanifolds de $\mathbb R^n$ pero se puede demostrar que es equivalente a la definición del espacio geométrico tangente al sumergir su colector en $\mathbb R^n$ (que siempre se puede hacer por Teorema de incrustación de Whitney ) y restringiendo su espacio "flecha" en cada punto al subespacio "flecha" de los vectores tangentes a $M$ como submanifold, del mismo modo que se puede pensar en los planos tangentes de una superficie en el espacio. Además esto se confirma por la transformación de componentes, si dos gráficos $x$ y $y$ contener el punto $p$ entonces sus vectores de coordenadas se transforman con la Jacobiano de la transformación de coordenadas $x\mapsto y$ : $$\frac{\partial}{\partial y^i}=\sum_{j=1}^n\frac{\partial x^j}{\partial y^i}\frac{\partial}{\partial x^j},$$ que da la regla de transformación anticuada para los vectores (y tensores) como se define en la física teórica. Ahora es un ejercicio fácil ver que, si un cambio de base en $V$ de $\vec e_i$ a $\vec e'_j$ viene dada por la matriz invertible $\Lambda^i_{j'}$ (que es siempre el caso), entonces las bases duales correspondientes están relacionadas por la transformación inversa $\Lambda^{j'}_i:=(\Lambda^i_{j'})^{-1}$ : $$\vec e'_j = \sum_{i=1}^n \Lambda^i_{j'}\,\vec e_i\Rightarrow \tilde e'^j = \sum_{i=1}^n (\Lambda^i_{j'})^{-1}\,\tilde e^i=:\sum_{i=1}^n \Lambda^{j'}_i\,\tilde e^i,\;\text{ where }\sum_i \Lambda^{k'}_i\Lambda^i_{j'}=\delta^{k'}_{j'}.$$ Así, en nuestro múltiple, el espacio cotangente se define como $T_p^*M$ con una base de coordenadas dada por los funcionales duales $\omega_{x}^i (\partial/\partial x^j)=\delta^i_j$ , $\omega_{y}^i (\partial/\partial y^j)=\delta^i_j$ . Por la ley de transformación de los vectores tangentes y la discusión anterior sobre la transformación dual, debemos tener que los covectores tangentes se transforman con la inversa del jacobiano anteriormente mencionado: $$\omega_y^i=\sum_{j=1}^n\frac{\partial y^i}{\partial x^j}\omega_x^j.$$ ¡Pero esta es precisamente la regla de transformación de las diferenciales por la regla de la cadena! $$dy^i=\sum_{j=1}^n\frac{\partial y^i}{\partial x^j}dx^j.$$ Por lo tanto, es convencional utilizar la notación $\partial/\partial x^i$ y $dx^i$ para la base de coordenadas del vector tangente y del covector en un gráfico $x:M\rightarrow\mathbb R^n$ .
Ahora, desde el punto de vista anterior $dx^i$ se consideran como los diferenciales clásicos, sólo que con la nueva perspectiva de ser los duales funcionales de los operadores diferenciales $\partial/\partial x^i$ . Para dar más sentido a esto, hay que recurrir a las formas diferenciales, que son nuestro $k$ -forma en $M$ . Una forma 1 $\omega\in T_p^*M=\Omega_p^1(M)$ es entonces sólo $$\omega = \sum_{i=1}^n \omega_i\, dx^i,$$ con $\omega_i(x)$ variando con $p$ campos escalares suaves sobre la variedad. Es habitual considerar $\Omega^0(M)$ el espacio de los campos escalares suaves. Tras definir productos alternativos en cuña obtenemos el $k$ -base del formulario $dx^i\wedge dx^j\in\Omega^2(M), dx^i\wedge dx^j\wedge dx^k\in\Omega^3(M),..., dx^1\wedge\cdots\wedge dx^n\in\Omega^n(M)$ (de hecho, no todas las combinaciones de índices para cada orden son independientes debido a la antisimetría, por lo que las bases tienen menos elementos que el conjunto de productos). Todos estos espacios lineales "cotensores" se juntan muy bien en un anillo con esa cuña $\wedge$ producto alterno, y se puede definir una bonita operación de diferenciación para dichos objetos: la derivada exterior $\mathbf d:\Omega^k(M)\rightarrow\Omega^{k+1}(M)$ dado por $$\mathbf d\omega^{(k)}:=\sum_{i_0<...<i_k}\frac{\partial\omega_{i_1,...,i_k}}{\partial x^{i_0}}dx^{i_0}\wedge dx^{i_1}\wedge\cdots\wedge dx^{i_k}.$$ Esta operación diferencial es una generalización de, y se reduce a, la habitual operadores de cálculo vectorial $\operatorname{grad},\,\operatorname{curl},\,\operatorname{div}$ en $\mathbb R^n$ . Así, podemos aplicar $\mathbf d$ para suavizar los campos escalares $f\in\Omega^0(M)$ para que $\mathbf df=\sum_i\partial_i f dx^i\in\Omega^1(M)$ (tenga en cuenta que no todos los covectores $\omega^{(1)}$ provienen de algunos $\mathbf d f$ una condición necesaria y suficiente para este "exactitud de las formas" es que $\partial_{i}\omega_j=\partial_{j}\omega_i$ para cualquier par de componentes; este es el comienzo de La cohomología de de Rham ). En particular, las funciones de coordenadas $x^i$ de cualquier gráfico satisfacen $$\mathbf d x^i=\sum_{j=1}^n\frac{\partial x^i}{\partial x^j}dx^j=\sum_{j=1}^n\delta^i_jdx^j= dx^i.$$
ESTA última igualdad establece la correspondencia entre las diferenciales infinitesimales $dx^i$ y las derivadas exteriores $\mathbf dx^i$ . Como podríamos haber escrito cualquier otro símbolo para la base de $\Omega_p^1(M)$ es evidente que $\mathbf dx^i$ son una base para el espacio tangente dual. En la práctica, la notación se reduce a $\mathbf d=d$ ya que estamos trabajando con objetos isomórficos a nivel de su álgebra lineal. Todo esto es la razón por la que $\mathbf dx^i(\partial_j)=\delta^i_j$ ya que una vez demostrado que el $\mathbf dx^i$ forman una base de $T_p^*M$ es sencillo sin recurrir a las leyes de transformación de los componentes. Por otro lado, se podría empezar después de la definición de los espacios tangentes como se ha dicho anteriormente, con la base de coordenadas $\partial/\partial x^i$ y dualizar a su base covectorial $\tilde e^i$ tal que $\tilde e^i(\delta_j)=\delta^i_j$ Después, se definen los productos cuña y las derivadas exteriores como es habitual en los espacios cotangentes; entonces es un teorema que para cualquier campo vectorial tangente $X$ y la función $f$ en $M$ $$X(f)=\sum_{i=1}^n X^i\frac{\partial f}{\partial x^i}=\mathbf d f(X),$$ por lo que en particular obtenemos como corolario que nuestra base de coordenadas dual original es de hecho la diferencial exterior de las funciones de coordenadas: $$(\vec e_i)^*=\tilde e^i=\mathbf d x^i\in\Omega^1(M):=T^*(M).$$ (Esto es cierto en cualquier punto para cualquier base de coordenadas de las cartas posibles, por lo que es cierto como campos covectores sobre el colector). En particular, la evaluación de los covectores $\mathbf d x^i$ en vectores infinitesimales $\Delta x^j\partial_j$ es $\mathbf d x^i(\Delta x^j\partial_j)=\sum_{j=1}^n\delta^i_j\Delta x^j$ Así que cuando $\Delta x^i\rightarrow 0$ podemos ver las diferenciales infinitesimales como las evaluaciones de vectores infinitesimales por covectores de coordenadas.
SIGNIFICADO, USO Y APLICACIONES:
Los covectores son la estructura esencial para las formas diferenciales en topología/geometría diferencial y la mayoría de los desarrollos importantes en esos campos están formulados o los utilizan de una manera u otra. Son ingredientes centrales de temas importantes como:
Dependencia lineal de vectores, determinantes e hipervolúmenes, orientación , integración de formularios ( Teorema de Stokes generalizando el teorema fundamental del cálculo), homología singular y grupos de cohomología de Rham ( El lema de Poincaré , Teorema de de Rham , Características de Euler y aplicaciones como invariantes para la topología algebraica), derivada covariante exterior , conexión y curvatura de los haces vectoriales y principales , clases características , Operadores laplacianos , funciones armónicas & Teorema de descomposición de Hodge , los teoremas del índice ( Chern-Gauß-Bonnet , Hirzebruch-Riemann-Roch , Atiyah-Singer ...) y una estrecha relación con los invariantes topológicos modernos (Donaldson-Thomas, Gromow-Witten, Seiberg-Witten, ecuaciones de solitón...).
En particular, desde el punto de vista de la física matemática, las formas diferenciales (covectores y tensores en general) son entidades fundamentales para la formulación de teorías físicas en términos geométricos. Por ejemplo, Ecuaciones de Maxwell del electromagnetismo son sólo dos ecuaciones de formas diferenciales en El espaciotiempo de Minkowski : $$\mathbf d F=0,\;\;\star\mathbf d\star F=J,$$ donde $F$ es un $2$ -(una matriz antisimétrica de 4x4) cuyos componentes son los componentes del campo vectorial eléctrico y magnético $E_i,\,B_j$ , $J$ es un vector espaciotemporal de densidades de carga-corriente y $\star$ es el Operador estrella de Hodge (que depende de la métrica de la variedad, por lo que requiere una estructura adicional). De hecho, la primera ecuación no es más que la formulación diferencial-geométrica de la clásica Ley de Gauß para el campo magnético y el Ley de inducción de Faraday . La otra ecuación es la dinámica Ley de Gauß para el campo eléctrico y Ley del circuito de Ampère . El ley de continuidad de la conservación de la carga se convierte en $\mathbf d\star J=0$ . Además, por El lema de Poincaré , $F$ siempre se puede resolver como $F=\mathbf d A$ con $A$ un covector en el espaciotiempo llamado potencial electromagnético (de hecho, en ingeniería eléctrica y telecomunicaciones siempre resuelven las ecuaciones por estos potenciales); ya que la diferenciación exterior satisface $\mathbf{d\circ d}=0$ los potenciales están subdeterminados por $A'=A+\mathbf d\phi$ , que es precisamente la más sencilla "invariancia gauge" que rodea todo el campo de la física. En la física teórica la fuerza electromagnética proviene de un $U(1)$ paquete principal sobre el espaciotiempo; generalizando esto para los grupos de Lie $SU(2)$ y $SU(3)$ se llega a los modelos matemáticos de las fuerzas nucleares débil y fuerte (teoría electrodébil y cromodinámica). El Faraday $2$ -forma $F$ es en realidad la curvatura local de la conexión gauge para esos haces de fibras, y de forma similar para las otras fuerzas. Este es el marco de Teoría de las galgas trabajando en colectores arbitrarios para su espaciotiempo. La única otra fuerza que queda es la gravedad, y de nuevo la relatividad general puede escribirse en la forma Formalismo de Cartan como una curvatura de un Conexión de espín de Lorentz sobre un $SO(1,3)$ o, de forma equivalente, como la curvatura (riemanniana) del haz espacial tangente.

 para centrarte en el "espacio de parámetros". Piensa en que tienes un modelo con una forma dada $$\alpha_1 \cdot \phi_1(\vec{x}) + \alpha_2 \cdot \phi_2(\vec{x}) + \alpha_3 \cdot \phi_3(\vec{x}) + \ldots$$ por ejemplo los $\phi_i$ podrían ser funciones de base. Ajustar los pesos $\alpha_i$ es el objetivo del modelado estadístico. Por ejemplo, la solución OLS elige un covector "óptimo" (en algún sentido de la palabra "óptimo").
para centrarte en el "espacio de parámetros". Piensa en que tienes un modelo con una forma dada $$\alpha_1 \cdot \phi_1(\vec{x}) + \alpha_2 \cdot \phi_2(\vec{x}) + \alpha_3 \cdot \phi_3(\vec{x}) + \ldots$$ por ejemplo los $\phi_i$ podrían ser funciones de base. Ajustar los pesos $\alpha_i$ es el objetivo del modelado estadístico. Por ejemplo, la solución OLS elige un covector "óptimo" (en algún sentido de la palabra "óptimo"). 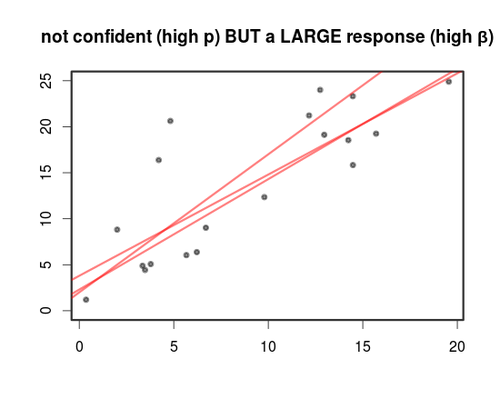 Y el descenso del gradiente en algún tipo de modelo que puede ser parametrizado por "sumas de ponderaciones de [cosas]" también apunta al mismo objetivo explorando el espacio de covectores.
Y el descenso del gradiente en algún tipo de modelo que puede ser parametrizado por "sumas de ponderaciones de [cosas]" también apunta al mismo objetivo explorando el espacio de covectores.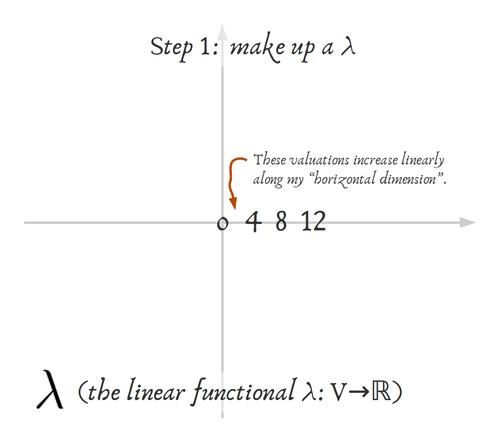

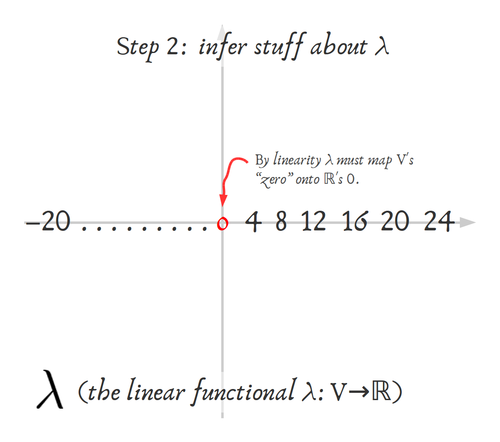

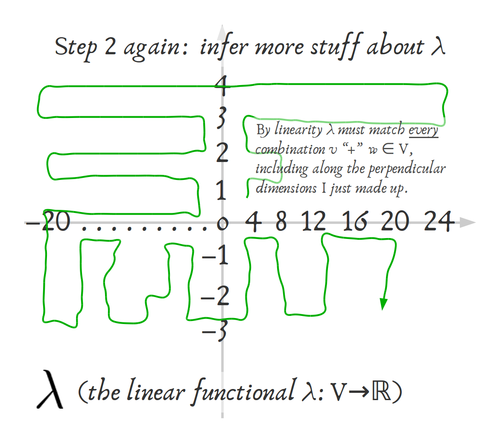



32 votos
Lo que siempre me resultó más confuso es el paso entre la situación de álgebra lineal y la situación infinitesimal. Si tenemos una base $\{x_1, \ldots, x_n\}$ para un espacio vectorial $V$, entonces la base dual $\{dx_1, \ldots, dx_n\}$ de $V^*$ se determina por $dx_i(a_1x_1 + \cdots + a_nx_n) = a_i$. Por supuesto, esta notación $dx_i$ es bastante desafortunada. De hecho, más o menos toda mi confusión en geometría diferencial (al menos hasta donde llegué) ha surgido de una mala notación.
5 votos
Sí, creo que la mayoría de mi malentendido surgió del hecho de que estaba interpretando $dx$ como una "longitud" en lugar de una función.
2 votos
Cuando dices que no puedes imaginar qué es $dx([1,2])$ ... ¿estás utilizando la notación $[1,2]$ para referirte a un vector en $\mathbb{R}^2$ con coordenadas $(1, 2)$? Eso sería bastante no estándar, así que pregunto solo para aclarar.
1 votos
Sí, entonces $dx([1,2])$ sería la función $dx$ actuando sobre el vector $[1,2] \in R^2$.
2 votos
También puedes llamarlos proyectores