Cuál es el volumen máximo de $N$-D rebanada de un $M$-D hipercubo?

Question

Considere la posibilidad de un hipercubo unidad de M dimensiones. Queremos hacer un corte de dimensión N a través de ella. ¿Cuál es el mayor N-D tamaño (longitud, área, volumen, ...) que lo podemos lograr, $S(M, N)$, y qué corte le da?

Ejemplos:

• $S(M=2, N=1) = \sqrt2$
  • Recorte lineal a través de un cuadrado
  • Tajada más grande es la diagonal
  • La longitud de la $\sqrt{1^2 + 1^2}$
• $S(M=3, N=1) = \sqrt3$
  • Recorte lineal a través de un cubo
  • Tajada más grande es el espacio en diagonal
  • La longitud de la $\sqrt{1^2 + 1^2 + 1^2}$
• $S(M=3, N=2) = \sqrt 2$
  • Plano de corte a través de un cubo
  • Tajada más grande es el plano a través de la diagonal
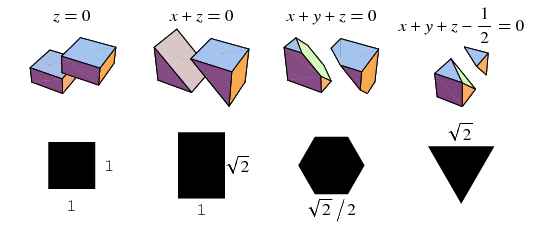
  • Área de $\sqrt 2 \cdot 1$

Los Bits de esta función son fáciles de generalizar: $$ S(M, N) = \left\{ \begin{array}{rl} \sqrt M & : N = 1\\ ? & : 1 < N < M\\ 1 & : N = M\\ 0 & : N > M\\ \end{array} \right. $$

Podemos generalizar para $N = 2, 3, ...$?

Answer 1

Como un límite inferior $S(M, N) \ge \sqrt{M - N + 1}$

donde la división es una $\underbrace{1 \times 1 \times \cdots}_{N-1} \times \sqrt{M - N + 1}$ cuboide

---

Elegir la primera, $N-1$ ejes de la hipercubo, se encuentra en el sector espacio. (Posiblemente no óptimo)

Un $M - N + 1$ subespacio sigue siendo, a partir de la cual queremos encontrar el más largo de la 1 de la zona.

Esto es $S(M - N + 1, 1) = \sqrt{M - N + 1}$.