Hay solo un espacio que en realidad es un paso bastante trivial si ya lo has visto antes. La primera línea es simplemente la representación integral de $n!$, la segunda línea es el teorema que queremos probar. La tercera y cuarta línea es una demostración abreviada de la representación integral de $n!$, dice que restar la función primitiva evaluada en cero da como resultado $n!$. Así que, hasta este punto no ha sucedido nada interesante aparte de la declaración del teorema. Luego lo que hace equivale a notar que:
$$\int_{0}^{\infty}x^{n-1}\exp\left(-r^kx\right)\;\mathrm{d}x = \frac{(n-1)!}{r^{nk}}$$
Por lo tanto,
$$\sum_{k=0}^{\infty}\frac{f^{(k)}(0)}{k!}\int_{0}^{\infty}x^{n-1}\exp\left(-r^kx\right)\;\mathrm{d}x = (n-1)!\sum_{k=0}^{\infty} \frac{f^{(k)}(0)}{k!}\frac{1}{r^{nk}}$$
que es lo que obtienes si sumas el término general de las expresiones dadas en las líneas 5 a 7. La suma en el lado derecho da como resultado (asumiendo que la función es analítica):
$$(n-1)! f\left(\frac{1}{r^n}\right)$$
Este es el lado derecho de la línea 10 después de la declaración "Sumando todos los resultados que tenemos". El espacio es cómo obtuvo el lado izquierdo. Pero esto es simplemente una cuestión de expandir el exponencial en la integral en potencias e intercambiar las dos sumatorias. Esto da como resultado:
$$\int_{0}^{\infty}\sum_{m=0}^{\infty}\sum_{k=0}^{\infty}(-1)^m r^{km} x^m\frac{f^{(k)}(0)}{k!m!}x^{n-1}\;\mathrm{d}x $$
La sumatoria sobre $k$ da como resultado:
$$\int_{0}^{\infty}\sum_{m=0}^{\infty}(-1)^m x^m\frac{f\left( r^{m}\right)}{m!}x^{n-1}\;\mathrm{d}x $$
que es el lado izquierdo de la línea diez. Podemos escribir la línea diez como:
$$\int_{0}^{\infty}x^{n-1}\sum_{m=0}^{\infty}(-1)^m x^m\frac{f\left( r^{m}\right)}{m!}\;\mathrm{d}x = (n-1)! f\left(\frac{1}{r^n}\right)$$
Luego, como dice la siguiente línea, es cuestión de poner $ f\left(r^n\right) = \phi(n)$ para obtener el teorema:
$$\int_{0}^{\infty}x^{n-1}\sum_{m=0}^{\infty}(-1)^m \frac{\phi\left(m\right)}{m!}x^m \;\mathrm{d}x = (n-1)!\phi\left(-n\right)$$
Derivaciones formales como esta que involucran solo manipulaciones de series de potencias pueden ser manejadas de manera más eficiente utilizando métodos de cálculo umbral, un caso especial del teorema maestro de Ramanujan que de hecho fue obtenido por Glaisher usando tales métodos (la última afirmación cr. 4 para $n = 0$). El cálculo umbral implica confundir deliberadamente subíndices de coeficientes como exponentes realizando los cálculos y luego al final devolviendo los índices a donde pertenecen. Entonces, en la integral:
$$\int_{0}^{\infty}x^{n-1}f(x) \;\mathrm{d}x$$
con
$$f(x) = \sum_{k=0}^{\infty}(-1)^k\frac{c_k}{k!}x^k$$
escribiríamos $f(x)$ como:
$$f(x) = \sum_{k=0}^{\infty}(-1)^k\frac{c^k}{k!}x^k = \exp(-c x)$$
Esto da como resultado:
$$\int_{0}^{\infty}x^{n-1}f(x) \;\mathrm{d}x = \int_{0}^{\infty}x^{n-1}\exp(-c x) \;\mathrm{d}x = \frac{(n-1)!}{c^n}$$
Y luego cambiamos el exponente de regreso a un índice, lo que da como resultado el teorema:
$$\int_{0}^{\infty}x^{n-1}f(x) \;\mathrm{d}x = (n-1)! c_{-n}$$

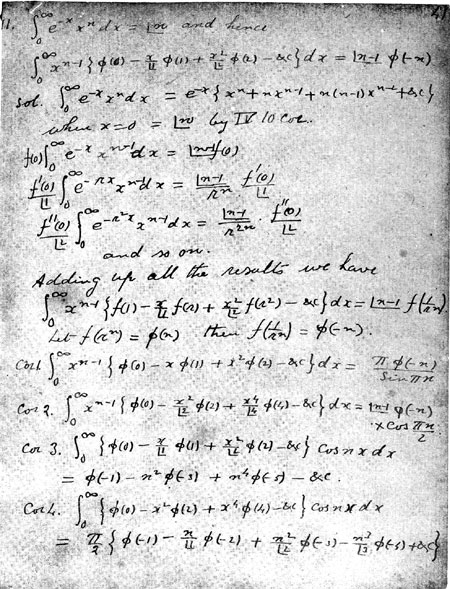



3 votos
Berndt discute la prueba de Ramanujan en Los Cuadernos de Ramanujan, Parte 1, página 298.
0 votos
@nospoon : ¿Puedes decirnos si se asume que $\phi(z)$ es entera o meromorfa?
1 votos
@nospoon ¡Gracias! ¿Puedes agregar eso como una respuesta para que ya no aparezca como sin responder?