¿Es un spinor de algún modo conectado al espacio?

Question

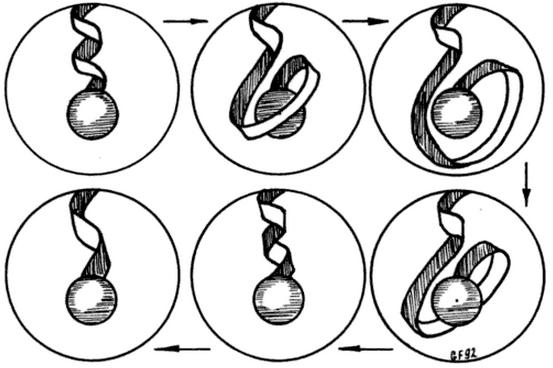
Spinors transformar en virtud de la representación de la $SL(2,\mathbb{C})$ que es el doble de la portada del grupo de Lorentz $SO(1,3)$ - o en la no-relativista caso en $SU(2)$, el doble de la cubierta de $SO(3)$.

Esto a menudo es visualizado a través de la Dirac cinturón de truco, la construcción de "spinorial objetos" con lasos con el espacio circundante. Pero ¿qué significa eso realmente?

• Son spinors de alguna manera conectado con el espacio-tiempo?
• Spinors mantener una "huella" de cómo han sido rotada (ruta de acceso la dependencia del/de la memoria) - ¿cómo es eso posible?
• Entiendo que la topológico argumento con simplemente la conexión de la universalización de la cobertura frente a la original de rotación de grupo - pero, ¿cómo puede una de Dirac partícula "sentido" de la topología?

• En la Dirac truco, la huella de la ruta de acceso (número de rotaciones) es claramente visible para todo el mundo por el número de vueltas en el cinturón! Así que no encuentre su "ruta de acceso de la memoria" tan misterioso como para la libre fermión. Un electrón es asumido sin estructura, sin cualquier interior grados de libertad, salvo spin - así que, ¿cómo puede "seguir la pista" el número $n$ de tergiversaciones igual que el cinturón conectado a algunos de fondo fijo?

  La distorsión/torsión de la correa está a la vista! Puedo contar simplemente buscando en el propio sistema. Esta distorsión es claramente una característica del sistema. Así que no es tan sorprendente que las dos situaciones (par o impar $n$) son distinguidos. Pero para un spinor, no hay tal cosa de seguir la pista de $n$ - libre de partículas de Dirac no interactúa con nada!

Estoy familiarizado con los argumentos usuales (homotopy clases, etc), pero esos no resolver mi problema/problemas para hacer sentido de spinorial objetos - por lo tanto necesita más ayuda. Muchas gracias!

Answer 1

No estamos del todo seguro de lo OP de la pregunta (v4) está pidiendo, pero aquí están algunos comentarios:

I) La Dirac cinturón truco demuestra que la Mentira de grupo $SO(3)$ de rotaciones 3D es doblemente conectado, $$ \pi_1(SO(3))~=~\mathbb{Z}_2. $$

II) en cuanto a la pregunta del título Se spinors de alguna manera conectado con el espacio-tiempo? una respuesta podría ser: Sí, en el sentido de que la mera existencia de spinors pone topológica de las restricciones sobre los posibles spacetimes. En detalle, la existencia de un mundo definido (Weyl) spinor en un (espacio-tiempo) colector $M$ tiene las siguientes topológico implicaciones para $M$:

1. El (espacio-tiempo) colector $M$ debe ser orientable, es decir, el 1 de Stiefel-Whitney clase $w_1(M)\in H^1(M,\mathbb{Z}_2)$ debe desaparecer.

2. La 2ª Stiefel-Whitney clase $w_2(M)\in H^2(M,\mathbb{Z}_2)$ debe desaparecer así, cf. por ejemplo, Wikipedia.

Answer 2

Usted también podría preguntar, "¿Cómo funciona la física de la correa en la Dirac truco sentido de la topología?" Esta pregunta es, cuando usted piensa acerca de ello, no menos misterioso que el tuyo. La respuesta, por medio de un experimento, es que simplemente lo hace.

Y en última instancia, si algo se transforma "compatible" con el grupo de Lorentz, o con $SO(3)$, entonces no es realmente sólo un bit pregunta: ¿estamos hablando de una representación del grupo original (es decir, $SO(3)$ o $SO^+(1,\,3)$) o su doble cobertura ($SU(2)$ o $SL(2,\,\mathbb{C})$)? No existen otras posibilidades (como usted probablemente sabe). La pregunta es prácticamente el mismo que para un electrón o de Dirac de la cinta.

El cinturón de Dirac es sólo una analogía física - aunque una bastante buena para un homotopy la clase por $C^1$ ruta de acceso a través de $SO(3)$ la vinculación de la identidad de un determinado $\gamma\in SO(3)$. Si usted idealizar la física de la correa a un conjunto de idealizaciones matemáticas que intuitivamente parecen bastante razonables (es decir, de acuerdo con nuestra intuición experimental obtenida de jugar con cintas y cinturones de Dirac), entonces sí, la analogía se convierte en exacta, como les comente en el Ejemplo 14.23 de mi artículo "la Mentira del Grupo Homotopy y Topología Global" en mi sitio web.

Pero entonces la pregunta es equivalente a preguntar ¿por qué el real, el objeto físico (Dirac correa) se comportan de la manera descrita por el matemático idealizaciones hablo en mi artículo. La respuesta es simplemente un totalmente experimental, a saber: simplemente hace, por experimental de inducción! No se puede cavar más profundo que esto.

Ahora, usted podría pedir un poco de la cuestión similar a lo largo de las líneas de "Podemos decir spinors se comportan como si ellos están vinculados con poco cintas para el espacio-tiempo, sólo en el sentido de ser matemáticamente análogo al de la matemática a la idealización de un cinturón de Dirac que, por ejemplo, puedo hablar?", entonces la respuesta es por supuesto que sí. Pero esta es una manera sutil, pero más claro que el agua, diferente a la de su pregunta.

Se puede decir entonces que cualquier experimentalmente spinorial objeto: electrones, cualquier tirada $\frac{1}{2}$ de partículas o de hecho de Dirac de la cinta es visto experimentalmente que parecen de alguna manera a mantener una "huella" de cómo han sido rotada (dependencia de la trayectoria y de la memoria). Cosas que mantienen a esta huella (es decir, recordar la homotopy de la clase) son, por definición, experimentalmente de forma análoga a un miembro de la universalización de la cobertura de $SO(3)$ o $SO^+(1,\,3)$.