Serie para envoltura de bisectores de área triángulo

Question

Las líneas que biseca el área de un triángulo que forman una envoltura, como se muestra en esta imagen

No es difícil mostrar que la relación de la zona de la roja deltoides para el área de un triángulo es $$\frac{3}{4} \log_e(2) - \frac{1}{2} \approx 0.01986.$$

Pero esto también es $$\sum_{n=1}^{\infty}\frac{1}{(4n-1)(4n)(4n+1)}.$$

¿Hay alguna conexión entre la serie y el deltoides? O es sólo una coincidencia?

(Pregunté esto en MathOverflow hace casi 18 meses y no obtuvo respuesta)

Answer 1

Desde $|\triangle BPQ|=\frac12\sin(B)|\overline{BP}||\overline{BQ}|$, para mantener la $|\triangle BPQ|=\frac12|\triangle ABC|$, tenemos $|\overline{BP}||\overline{BQ}|=\tfrac12|\overline{BC}||\overline{BA}|$.

$\hspace{3.4cm}$

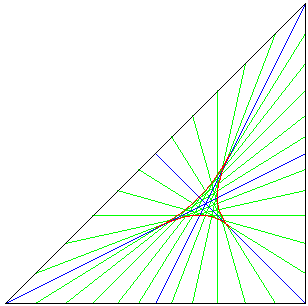
En el diagrama anterior, los puntos finales de las líneas son parametrizadas por $$ P_t=\frac{1-t}2B+\frac{1+t}2C\etiqueta{1} $$ y $$ Q_t=\frac{t}{1+t}B+\frac1{1+t}\etiqueta{2} $$ para $t\in[0,1]$.

Los puntos en cada línea son parametrizadas por $$ R_t(s)=(1-s)P_t+sQ_t\etiqueta{3} $$ Para encontrar un punto en la envolvente de la familia de las líneas de parametrizadas por $t$ tenemos que encontrar donde $$ \frac{\partial}{\partial t}R_t(s)=\frac{1-s}2(C-B)+\frac{s}{(1+t)^2}(B-A)\etiqueta{4} $$ es paralela a la $$ \frac{\partial}{\partial s}R_t(s)=\frac1{1+t}(a-B)+\frac{1+t}2(B-C)\etiqueta{5} $$ Configuración de la cruz del producto a $0$, obtenemos que $$ \frac{1-s}{2(1+t)}-\frac{s}{2(1+t)}=0\etiqueta{6} $$ que pasa cuando el $s=\frac12$. Es decir, el locus de la envolvente de los puntos medios de los segmentos de línea $$ M_t=B+\frac{1+t}4(C-B)+\frac1{2(1+t)}(a-B)\etiqueta{7} $$ $\hspace{3.4cm}$

Restando el centro del triángulo (y de los deltoides) en $M_\triangle=\frac13(A+B+C)$ rendimientos $$ M_t-M_\triangle=\left(\frac{1+t}4-\frac13\right)(C-B)+\left(\frac1{2(1+t)}-\frac13\right)(A-B)\tag{8} $$ Por lo tanto, $3$ veces el área de $\frac13$ de los deltoides es $$ \begin{align} &\frac32\int_0^1(M_t-M_\triangle)\times(M_t-M_\triangle)'\,\mathrm{d}t\\ &=3|\triangle ABC|\int_0^1\left[\frac14\left(\frac1{2(1+t)}-\frac13\right)+\frac1{2(1+t)^2}\left(\frac{1+t}4-\frac13\right)\right]\,\mathrm{d}t\\ &=\frac{3\log(2)-2}{4}|\triangle ABC|\tag{9} \end{align} $$ donde $|\triangle ABC|=\frac12|(A-B)\times(C-B)|$.

Desde el deltoides, como parametrizadas en $(7)$, es una combinación convexa de los vértices, se transforma con cualquier afín transformación lineal de los vértices. Por lo tanto, la relación de áreas no depende de la particular ubicación de los vértices.

---

$$ \begin{align} \sum_{k=1}^\infty\frac1{(4k-1)4k(4k+1)} &=\frac12\sum_{k=1}^\infty\left(\frac1{4k-1}-\frac1{2k}+\frac1{4k+1}\right)\\ &=\lim_{n\to\infty}\frac12\left(\color{#C00000}{\sum_{k=1}^{2n}\frac1{2k+1}-\sum_{k=1}^{2n}\frac1{2k}}+\color{#00A000}{\sum_{k=n+1}^{2n}\frac1{2k}}\right)\\ &=\frac12\left(\color{#C00000}{\log(2)-1}+\color{#00A000}{\frac12\log(2)}\right)\\[3pt] &=\frac{3\log(2)-2}{4}\tag{10} \end{align} $$

---

Por lo tanto, hemos $$ \begin{align} &3\int_0^1\left[\frac14\left(\frac1{2(1+t)}-\frac13\right)+\frac1{2(1+t)^2}\left(\frac{1+t}4-\frac13\right)\right]\,\mathrm{d}t\\[6pt] &=\frac{3\log(2)-2}{4}\\[6pt] &=\sum_{k=1}^\infty\frac1{(4k-1)4k(4k+1)} \end{align} $$ Tal vez hay otra manera de calcular el área del deltoides que hace que se convierta en la suma. Sin embargo, se ve como una coincidencia de este enfoque.